
【题目】关于二次函数![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.当![]() 时,
时,![]() 随
随![]() 的增大而减小B.它的图象与
的增大而减小B.它的图象与![]() 轴有交点
轴有交点
C.当![]() 时,
时,![]() D.它的图象与
D.它的图象与![]() 轴交于点
轴交于点![]()
【答案】C
【解析】
A. 根据对称轴及开口方向可判断;
B. 令y=0,解一元二次方程,可判断;
C. 通过抛物线与x轴的交点,结合开口方向可判断;
D. 令x=0,求出y值,可判断.
解:在函数y=x2-4x+3中a=1>0,
∴此函数图象开口向上;
又∵a=1,b=-4,c=3,
![]()
∴顶点坐标是(2,-1),且对称轴是x=2,
当x<1时,即说明x的取值范围在对称轴的左边,
∴y随x的增大而减小,故A正确,不符合题意;
∴令x2-4x+3=0,
解得x1=1,x2=3,
∴此函数图象和x轴有交点,求交点坐标是(1,0);(3,0).
故B正确,不符合题意;
当1<x<3时,抛物线在x轴下方,
∴y<0,故C错误,符合题意;
当x=0时,y=3,
∴抛物线与![]() 轴交于点
轴交于点![]() ,故D正确,不符合题意.
,故D正确,不符合题意.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,点O在ABCD的AD边上,⊙O经过A、B、C三点,点E在⊙O外,且OE⊥BC,垂足为F.
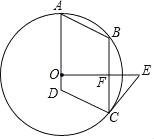
(1)若EC是⊙O的切线,∠A=65°,求∠ECB的度数;
(2)若OF=4,OD=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=CB,点E,F分别是AC,BC上的点,△CEF的外接圆交AB于点Q,D.
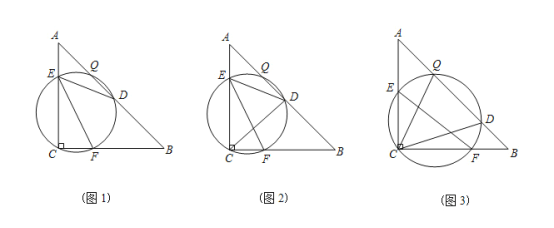
(1)如图1,若点D为AB的中点,求证:∠DEF=∠B;
(2)在(1)问的条件下:
①如图2,连结CD,交EF于H,AC=4,若△EHD为等腰三角形,求CF的长度.
②如图2,△AED与△ECF的面积之比是3:4,且ED=3,求△CED与△ECF的面积之比(直接写出答案).
(3)如图3,连接CQ,CD,若AE+BF=EF,求证:∠QCD=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解: ![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
根据你的观察,探究下面的问题:
(1)己知![]() ,求
,求![]() 的值.
的值.
(2)已知△ABC的三边长a、b、c都是正整数,且满足![]() ,求边c的最大值.
,求边c的最大值.
(3) 若己知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为_____.
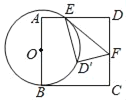
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
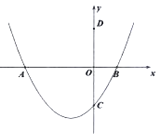
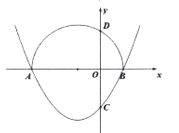
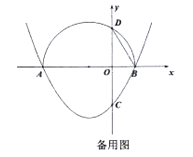
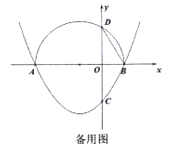
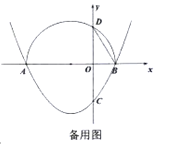
(1)直接写出抛物线的对称轴,及抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标;
的坐标;
(2)点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,当点
,当点![]() 在以
在以![]() 为直径的半圆上时,求抛物线的解析式;
为直径的半圆上时,求抛物线的解析式;
(3)在(2)的情况下,在抛物线上是否存在一点![]() ,使
,使![]() ,
,![]() ,
,![]() 三条之中,其中一条是另两条所夹角的角平分线?若存在,请求出点
三条之中,其中一条是另两条所夹角的角平分线?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
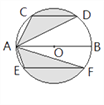
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一圆弧形桥拱的圆心为![]() ,拱桥的水面跨度
,拱桥的水面跨度![]() 米,桥拱到水面的最大高度
米,桥拱到水面的最大高度![]() 为
为![]() 米.求:
米.求:

![]() 桥拱的半径;
桥拱的半径;
![]() 现水面上涨后水面跨度为
现水面上涨后水面跨度为![]() 米,求水面上涨的高度为________米.
米,求水面上涨的高度为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)甲乙两人在相同条件下完成了5次射击训练,两人的成绩如图所示.
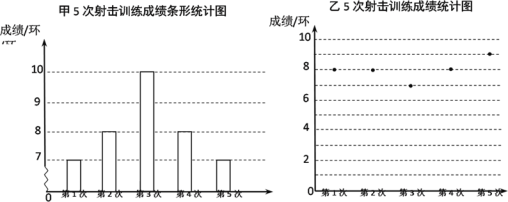
(1)甲射击成绩的众数为 环,乙射击成绩的中位数为 环;
(2)计算两人射击成绩的方差;
(3)根据训练成绩,你认为选派哪一名队员参赛更好,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com