
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(1,0),B(0,![]() ),则以AB为边的“坐标菱形”的最小内角为______;
),则以AB为边的“坐标菱形”的最小内角为______;
(2)若点C(2,1),点D在直线y=5上,以CD为边的坐标菱形”为正方形,求育直线CD表达式;
(3)⊙O的半径为![]() ,点P的坐标为(3,m),若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m),若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
【答案】(1)60°;(2)y=x-1或y=-x+3;(3)m的取值范围是1≤m≤5或-5≤m≤-1.
【解析】
(1)根据定义建立以AB为边的“坐标菱形”,由勾股定理求边长AB=4,可得30度角,从而得最小内角为60°;
(2)先确定直线CD与直线y=5的夹角是45°,得D(6,5)或(-2,5),易得直线CD的表达式为:y=x-1或y=-x+3;
(3)分两种情况:①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3,根据等腰直角三角形的性质分别求P'B=BD=1,PB=5,写出对应P的坐标;
②先作直线y=-x,再作圆的两条切线,且平行于直线y=-x,如图4,同理可得结论.
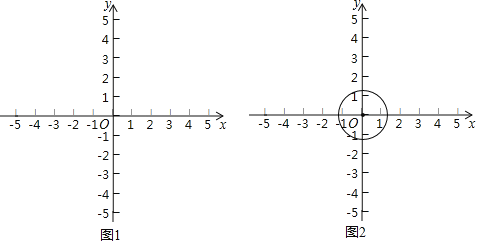
解:(1)如图1中,
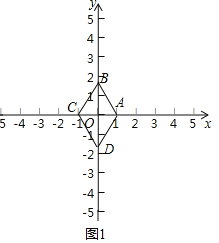
点A(1,0),B(0,![]() ),
),
∴OA=1,OB=![]() ,
,
在Rt△AOB中,由勾股定理得:AB=![]() =2,
=2,
∵sin∠ABO=![]() =
=![]() ,
,
∴∠ABO=30°,
∵四边形ABCD是菱形,
∴∠ABC=2∠ABO=60°,
∵AB∥CD,
∴∠DCB=180°-60°=120°,
∴以AB为边的“坐标菱形”的最小内角为60°,
故答案为:60°;
(2)如图2中,
∵以CD为边的“坐标菱形”为正方形,
∴直线CD与直线y=5的夹角是45°.
过点C作CE⊥DE于E.
∴D(6,5)或(-2,5).
∴直线CD的表达式为:y=x-1或y=-x+3;
(3)分两种情况:
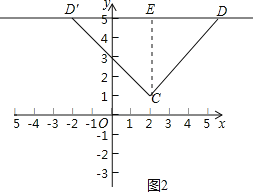
①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3,
∵⊙O的半径为![]() ,且△OQ'D是等腰直角三角形,
,且△OQ'D是等腰直角三角形,
∴OD=![]() OQ'=2,
OQ'=2,
∴P'D=3-2=1,
∵△P'DB是等腰直角三角形,
∴P'B=BD=1,
∴P'(0,1),
同理可得:OA=2,
∴AB=3+2=5,
∵△ABP是等腰直角三角形,
∴PB=5,
∴P(0,5),
∴当1≤m≤5时,以QP为边的“坐标菱形”为正方形;
②先作直线y=-x,再作圆的两条切线,且平行于直线y=-x,如图4,
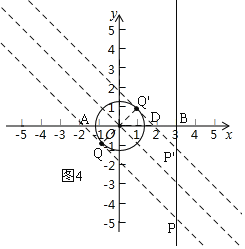
∵⊙O的半径为![]() ,且△OQ'D是等腰直角三角形,
,且△OQ'D是等腰直角三角形,
∴OD=![]() OQ'=2,
OQ'=2,
∴BD=3-2=1,
∵△P'DB是等腰直角三角形,
∴P'B=BD=1,
∴P'(0,-1),
同理可得:OA=2,
∴AB=3+2=5,
∵△ABP是等腰直角三角形,
∴PB=5,
∴P(0,-5),
∴当-5≤m≤-1时,以QP为边的“坐标菱形”为正方形;
综上所述,m的取值范围是1≤m≤5或-5≤m≤-1.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2017的横坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
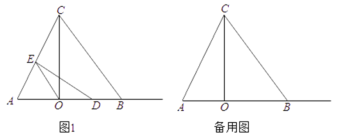
(1)求![]() ,
,![]() 的长
的长
(2)若点![]() 是射线
是射线![]() 上的一个动点,作
上的一个动点,作![]() 于点
于点![]() ,连结
,连结![]() .
.
①当点![]() 在线段
在线段![]() 上时,若
上时,若![]() 是以
是以![]() 为腰的等腰三角形,请求出所有符合条件的
为腰的等腰三角形,请求出所有符合条件的![]() 的长.
的长.
②设![]() 交直线
交直线![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的长为______________.(直接写出结果)
的长为______________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
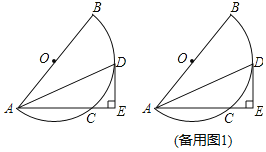
【题目】如图,AB为半圆的直径,O为半圆的圆心,AC是弦,取弧![]() 的中点D,过点D作DE⊥AC交AC的延长线于点E.
的中点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)当AB=10,AC=5时,求CE的长;
(3)连接CD,AB=10.当![]() =
=![]() 时,求DE的长.
时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() 是边
是边![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则有以下四个结论:①
,则有以下四个结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() 的周长是10;④
的周长是10;④![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
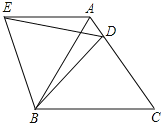
A.②③④B.①③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,AB=6,sinC=![]() ,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于
,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于![]() BM长为半径作弧,两弧相交于点N,射线AN与BC相交于D,则AD的长为_____.
BM长为半径作弧,两弧相交于点N,射线AN与BC相交于D,则AD的长为_____.
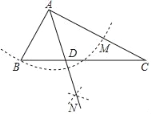
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,已知BC=40cm,AD=30cm,求这个正方形的边长.
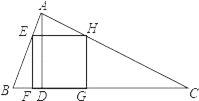
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com