
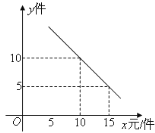
����Ŀ��ij�ľ����۵����������г�ѡ��A��B�����ľߣ�������A��Ϊ12Ԫ/����B��Ϊ8Ԫ/�������õ�����A��B�����ľߵ���������y�����������ۼ�x��Ԫ/��������һ�κ�����ϵ������ͼ��
��1����y��x�ĺ�����ϵʽ��
��2���õ�ƻ����ѡ��A��B�����ľߵ�������120���������ʽ���1200Ԫ����ϣ��ȫ���������������178Ԫ������A���ľ���������6����B���ľ�ÿ���ɻ���1Ԫ���㣬��õ�������ļ��ֽ���������
��3����A���ľߵ����ۼ۱�B���ľߵ����ۼ۸�4Ԫ/�����������ľ�ÿ�����������Ԫ����A���ľ����ۼ�x��Ԫ/����֮��ĺ�����ϵʽ����˵��A��B�����ľ����ۼ۷ֱ�Ϊ����ʱ��ÿ�����۵��������
���𰸡���1��![]() ����2�������ֽ����������ֱ�������
����2�������ֽ����������ֱ�������![]() ��58����
��58����![]() ��62��������
��62��������![]() ��59����
��59����![]() ��61��������
��61��������![]() ��60����
��60����![]() ��60������3��
��60������3��![]() ��
��![]() �ľ����ۼ�Ϊ16Ԫ��
�ľ����ۼ�Ϊ16Ԫ��![]() �ľ����ۼ�Ϊ12Ԫʱ�������
�ľ����ۼ�Ϊ12Ԫʱ�������
��������
��1���ô���ϵ���������ʽ��
��2�����������![]() ���ľ�
���ľ�![]() ���������������ȡֵ��Χ�����ʵ�����ȡ��������⣻
���������������ȡֵ��Χ�����ʵ�����ȡ��������⣻
��3������A���ľߵ����ۼ۱�B���ľߵ����ۼ۸�4Ԫ/����A���ľ����ۼ�x��Ԫ/��������B���ľ����ۼۣ�x-4����Ԫ/������ÿ��A���ľߵ�����Ϊ��x-12��Ԫ��ÿ��B���ľߵ�����Ϊ��x-4-8��Ԫ���ݴ��г����̣�Ȼ�ɵõ������
�⣺��1����ͼ��֪����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
��![]() ����������ã�
����������ã�![]() ��
��
���![]() ��
��
![]() ��
��
��2����![]() ʱ����
ʱ����![]() ����
����![]() ���ۼ�Ϊ14Ԫ��
���ۼ�Ϊ14Ԫ��
���������![]() ���ľ�
���ľ�![]() ������
������![]() �ľ���
�ľ���![]() ���������⣬��
���������⣬��![]() ��
��
���![]() ��
��
���ľߵ�����Ϊ������
�������ֽ����������ֱ�������![]() ��58����
��58����![]() ��62��������
��62��������![]() ��59����
��59����![]() ��61��������
��61��������![]() ��60����
��60����![]() ��60����
��60����
��3����A���ľߵ����ۼ۱�B���ľߵ����ۼ۸�4Ԫ/����A���ľ����ۼ�x��Ԫ/����
��B���ľ����ۼۣ�x-4����Ԫ/������ÿ��A���ľߵ�����Ϊ��x-12��Ԫ��ÿ��B���ľߵ�����Ϊ��x-4-8��Ԫ��
�������ľ�ÿ�����������![]() ��
��
��������![]() ��
��
��![]() �������ľ�ÿ����������������ֵ����ÿ�����۵��������
�������ľ�ÿ����������������ֵ����ÿ�����۵��������
��![]() �ľ����ۼ�Ϊ16Ԫ��
�ľ����ۼ�Ϊ16Ԫ��![]() �ľ����ۼ�Ϊ12Ԫʱ�������
�ľ����ۼ�Ϊ12Ԫʱ�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����̽�����֣�
��ͼ1��![]() �Ķ���
�Ķ���![]() ��������
��������![]() �����Խ��ߵĽ��㴦��
�����Խ��ߵĽ��㴦��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ת����ת�����У�
��ת����ת�����У�![]() �����߷ֱ���������
�����߷ֱ���������![]() �ı�
�ı�![]() ��
��![]() ���ڵ�
���ڵ�![]() �͵�
�͵�![]() ����
����![]() ���
���![]() ��
��![]() ���غϣ�����
���غϣ�����![]() ֮�������������ϵ���� ����
֮�������������ϵ���� ����
��2�������Ӧ�ã�
��ͼ2��������1���еġ�������![]() ����Ϊ��
������![]() ������
������![]() ���������������䣬��
���������������䣬��![]() ʱ�����������Ƿ���Ȼ�������������������֤���������������������۲�˵�����ɣ�
ʱ�����������Ƿ���Ȼ�������������������֤���������������������۲�˵�����ɣ�
��3������չ���죩
��ͼ3��![]() ��
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ��һ�㣬
��һ�㣬![]() ����
����![]() �ij���
�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ǽ�������ǣ� ����
A.�����ε����ĵ���������������ľ�����ȣ�
B.������������ε����߳��ֱ���5��6����ô������������ε��ܳ�Ϊ16��
C.��һ�κ���y��5x��1��ͼ������ƽ��3����λ������ֱ�߲������������ޣ�
D.������x��һԪһ�β���ʽ��![]() �⣬��m��ȡֵ��Χ��m��1��
�⣬��m��ȡֵ��Χ��m��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ��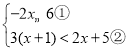 ����������գ���ɱ���Ľ��
����������գ���ɱ���Ľ��
�������ⲻ��ʽ�������� ����
�������ⲻ��ʽ�������� ����
�������Ѳ���ʽ�������Ľ��������ϱ�ʾ������
������ԭ����ʽ��Ľ⼯Ϊ�� ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��x�ύ�ڵ�A(-1��0)����������(1��n)����y��Ľ�����(0��2)��(0��3)֮�䣨�������˵㣩�������н��ۣ���a+b=0����
��x�ύ�ڵ�A(-1��0)����������(1��n)����y��Ľ�����(0��2)��(0��3)֮�䣨�������˵㣩�������н��ۣ���a+b=0����![]() ��������(-2��y1)��
��������(-2��y1)��![]() ��(2��y3)�ڴ��������ϣ���y1��y2��y3���ܵ�1<x<3ʱ������ax2+bx+c>0���ݹ���x�ķ���ax2+bx+c=n-1����������ȵ�ʵ��������ȷ���ǣ� ��
��(2��y3)�ڴ��������ϣ���y1��y2��y3���ܵ�1<x<3ʱ������ax2+bx+c>0���ݹ���x�ķ���ax2+bx+c=n-1����������ȵ�ʵ��������ȷ���ǣ� ��
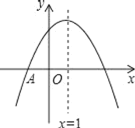
A.�٢ڢܢ�B.�٢ڢۢ�C.�ܢ�D.�ڢۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
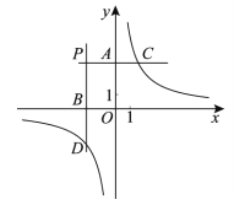
����Ŀ����ͼ���ֱ���ڶ������ڵĵ�![]() ��
��![]() ��
��![]() ���ƽ���ߣ���
���ƽ���ߣ���![]() ��
��![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����˫����
����˫����![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ��
��
�����������ۣ�
�ٴ�����������![]() ʹ
ʹ![]() ��
��
�ڴ�����������![]() ʹ
ʹ![]() ��
��
�۴�����������![]() ʹ
ʹ![]() ��
��
������ȷ���۵������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C = 90������O��б��AB��һ���㣬����O�ľ������OB�����е����ͼ��W��ͼ��W��AB��BC�ֱ��ڵ�D��E������AE��DE����AED=��B��

��1���ж�ͼ��W��AE����ֱ�ߵĹ������������֤����
��2����![]() ��
��![]() ����OB��
����OB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣨
���㣨![]() ��λ��
��λ��![]() ����ࣩ����
����ࣩ����![]() �ύ��
�ύ��![]() �㣬����
�㣬����![]() ����
����![]() Ϊ�����ߵĶ��㣬��
Ϊ�����ߵĶ��㣬��![]() Ϊ
Ϊ![]() ��
��

��1����![]() �ǵ����������������ϵ�һ�㣬����
�ǵ����������������ϵ�һ�㣬����![]() ��
��![]() �ύ�������ڵ�
�ύ�������ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() �ұߣ���
�ұߣ���![]() ��ֱ��
��ֱ��![]() ��һ�����㣬��
��һ�����㣬��![]() ��ֱ��
��ֱ��![]() ��һ�����㣬���ı���
��һ�����㣬���ı���![]() ���ܳ����ʱ����
���ܳ����ʱ����![]() ����Сֵ��
����Сֵ��
��2����ͼ2����ԭ����������Գ�����![]() ��Ľ���
��Ľ���![]() ��ת
��ת![]() ���µ�������
���µ�������![]() ����
����![]() ��
��![]() �Ķ�Ӧ��ֱ��Ϊ
�Ķ�Ӧ��ֱ��Ϊ![]() ��
��![]() ����������
����������![]() ��ֱ��
��ֱ��![]() ƽ�ƣ�
ƽ�ƣ�![]() ��
��![]() �Ķ�Ӧ��ֱ��Ϊ
�Ķ�Ӧ��ֱ��Ϊ![]() ��
��![]() �Ƿ���ڵ�
�Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ����
����![]() Ϊ���ĵ��������Σ������ڣ���ֱ��д��
Ϊ���ĵ��������Σ������ڣ���ֱ��д��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABDE��ƽ���ı��Σ�CΪ��B D�ӳ�����һ�㣬����AC��CE��ʹAB=AC��
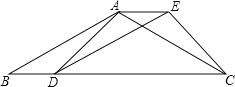
��1����֤����BAD�ա�AEC��
��2������B=30������ADC=45����BD=10����ƽ���ı���ABDE�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com