
如图,四边形ABCD为矩形,AB=4,AD=3,动点M从D点出发,以1个单位/秒的速度沿DA向终点A运动,同时动点N从A点出发,以2个单位/秒的速度沿AB向终点B运动.当其中一点到达终点时,运动结束.过点N作NP⊥AB,交AC于点P1连结MP.已知动点运动了x秒.
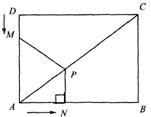
(1)请直接写出PN的长;(用含x的代数式表示)
(2)试求△MPA的面积S与时间x秒的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)在这个运动过程中,△MPA能否为一个等腰三角形.若能,求出所有x的对应值;若不能,请说明理由.![]()
解:(1)PN=![]() .
.
(2)过点P作PQ⊥AD交AD于点Q.
可知PQ=AN=2x.
依题意,可得AM=3-x.
∴S=![]() ·AM·PQ=
·AM·PQ=![]() ·(3-x)·2x=-x2+3x=-
·(3-x)·2x=-x2+3x=-![]() .
.
自变量x的取值范围是:0<x≤2.
∴当x=![]() 时,S有最大值,S最大值=
时,S有最大值,S最大值=![]() .
.
(3)△MPA能成为等腰三角形,共有三种情况,以下分类说明:
![]() ①若PM=PA,
①若PM=PA,
∵PQ⊥AD,∴MQ=QA=PN=![]() .
.
又DM+MQ+QA=AD ∴4x=3,即![]() x=
x=![]() .
.
②若MP=AM,
MQ=AD-AQ-DM=3-![]() ,PQ=2x,MP=MA=3-x.
,PQ=2x,MP=MA=3-x.
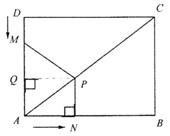 在Rt△PMQ中,由勾股定理得:MP2=MQ2+PQ2.
在Rt△PMQ中,由勾股定理得:MP2=MQ2+PQ2.
∴(3-x)2=(3-![]() )2+(2x)2.
)2+(2x)2.
解得x=![]() ,x=0(不合题意,舍去)
,x=0(不合题意,舍去)
③若AP=AM,
由题意可求AP=![]() ,AM=3-x.
,AM=3-x.
∴![]() =3-x.解得x=
=3-x.解得x=![]() .
.
综上所述,当x=![]() ,或x=
,或x=![]() ,或x=
,或x=![]() 时,△MPA是等腰三角形.
时,△MPA是等腰三角形.


科目:初中数学 来源: 题型:
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com