
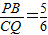 时,△APB的外接圆及内切圆的面积.(π≈3.14,
时,△APB的外接圆及内切圆的面积.(π≈3.14,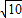 ≈3.16,
≈3.16,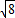 ≈2.83.结果精确到1cm2)
≈2.83.结果精确到1cm2)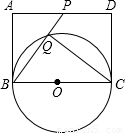
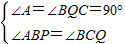
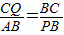 ,即
,即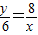 .
.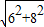 =10,
=10, .(6<x<10);
.(6<x<10);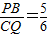 ,∴CQ=
,∴CQ= PB.
PB.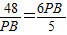 ,解得PB=2
,解得PB=2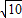 .
.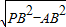 =2.
=2.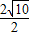 )2=10π≈31cm2.
)2=10π≈31cm2.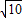 )r=6×2.
)r=6×2.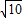 .
. )2=(26-8
)2=(26-8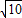 )π≈2cm2.
)π≈2cm2.

科目:初中数学 来源:2003年全国中考数学试题汇编《投影与视图》(01)(解析版) 题型:解答题
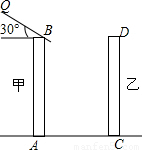 (2003•甘肃)如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况.
(2003•甘肃)如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况. =1.73);
=1.73);查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《锐角三角函数》(04)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《圆》(13)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《圆》(12)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com