
【题目】如图,已知 ![]() ,
, ![]() 是直线
是直线 ![]() 上的点,
上的点, ![]() ,过点
,过点 ![]() 作
作 ![]() ,并截取
,并截取 ![]() ,连接
,连接 ![]() ,判断△
,判断△ ![]() 的形状并证明.
的形状并证明.
【答案】解:△CDF是等腰直角三角形.证明如下:
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC.
在△FAD与△DBC中,∵AD=BC,∠FAD=∠DBC,AF=BD,
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形.
∵△FAD≌△DBC,
∴∠FDA=∠DCB.
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形
【解析】利用SAS证明△FAD≌△DBC可得FD=DC,从而得到△CDF是等腰三角形.再由△FAD≌△DBC,则∠FDA=∠DCB,可证得∠BDC+∠FDA=90°,从而证出△CDF的形状.
【考点精析】本题主要考查了等腰直角三角形的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能正确解答此题.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
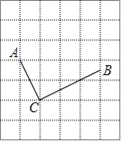
【题目】如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.
(Ⅰ)计算AB的长等于_____;
(Ⅱ)若点P,Q分别为线段BC,AC上的动点,且BP=CQ,请在如图所示的网格中,用无刻度的直尺,画出当PQ最短时,点P,Q的位置,并简要说明画图方法(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要设计一块面积为10平方米的正方形广告牌,公司在设计广告时,必须知道这个正方形的边长.这个正方形的边长是多少?估计边长的值(结果精确到十分位).
查看答案和解析>>
科目:初中数学 来源: 题型:
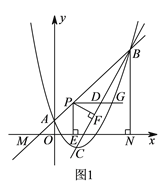
【题目】如图![]() ,二次函数
,二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限内,点
在第一象限内,点![]() 是二次函数图象的顶点,点
是二次函数图象的顶点,点![]() 是一次函数
是一次函数![]() 的图象与
的图象与![]() 轴的交点,过点
轴的交点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,且
,且![]() .
.
(![]() )求直线
)求直线![]() 和直线
和直线![]() 的解析式.
的解析式.
(2)点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 是线段
是线段![]() 上一点,
上一点, ![]() 轴,射线
轴,射线![]() 与抛物线交于点
与抛物线交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
, ![]() 于点
于点![]() ,当
,当![]() 与
与![]() 的乘积最大时,在线段
的乘积最大时,在线段![]() 上找一点
上找一点![]() (不与点
(不与点![]() ,点
,点![]() 重合),使
重合),使![]() 的值最小,求点
的值最小,求点![]() 的坐标和
的坐标和![]() 的最小值.
的最小值.
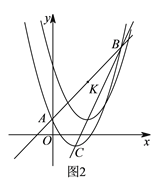
(![]() )如图
)如图![]() ,直线
,直线![]() 上有一点
上有一点![]() ,将二次函数
,将二次函数![]() 沿直线
沿直线![]() 平移,平移的距离是
平移,平移的距离是![]() ,平移后抛物线使点
,平移后抛物线使点![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,点
,点![]() ;当
;当![]() 是直角三角形时,求t的值.
是直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某中学为迎接校运会,筹集7000元购买了甲、乙两种品牌的篮球共30个,其中购买甲品牌篮球花费3000元,已知甲品牌篮球比乙品牌篮球的单价高50%,求乙品牌篮球的单价及个数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 的纵坐标满足
的纵坐标满足![]() , 则称点
, 则称点![]() 是点
是点![]() 的“绝对点”.
的“绝对点”.
(![]() )点
)点![]() 的“绝对点”的坐标为.
的“绝对点”的坐标为.
(![]() )点
)点![]() 是函数
是函数![]() 的图像上的一点,点
的图像上的一点,点![]() 是点
是点![]() 的“绝对点”.若点
的“绝对点”.若点![]() 与点
与点![]() 重合,求点
重合,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 的“绝对点”
的“绝对点”![]() 是函数
是函数![]() 的图像上的一点.当
的图像上的一点.当![]() 时,求线段
时,求线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的一点,过点F 作FG⊥BC于G点,并交AB于E点.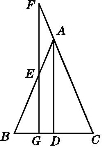
(1)求证:AD∥FG;
(2)△AFE为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com