
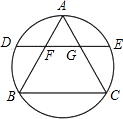
 如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为
如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为 解:过O点作OH⊥BC,垂足为H,连接OB,
解:过O点作OH⊥BC,垂足为H,连接OB, BC=6,∠OBH=
BC=6,∠OBH= ∠ABC=30°,
∠ABC=30°, =4
=4 ,
, ≈13.8,
≈13.8, ,
,

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
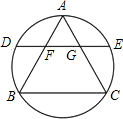 如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为( )
如图,边长为12的正三角形ABC内接于圆,弦DE∥BC分别交AB,AC于F,G,若AF长x,DF长y都是正整数,则y的值为( )| A、2 | B、3 | C、4 | D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
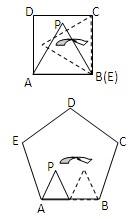 16、如图,已知正方形ABCD的边长AB=1,正△PAE的边长AE=1,开始时正△PAE与正方形ABCD边AB重合,顶点P在正方形内,将正△PAE在正方形内按如图所示的方式,沿着正方形的边AB、BC、CD、DA、AB、BC…连续地翻转
16、如图,已知正方形ABCD的边长AB=1,正△PAE的边长AE=1,开始时正△PAE与正方形ABCD边AB重合,顶点P在正方形内,将正△PAE在正方形内按如图所示的方式,沿着正方形的边AB、BC、CD、DA、AB、BC…连续地翻转查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•丹徒区模拟)用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y=
(2012•丹徒区模拟)用两个边长为1的正六边形拼接成如图(a)的图形,其周长为10;用三个边长为1的正六边形可以拼接成如图(b)或(c)的图形,其周长分别为12和14.若要拼接成周长为18的图形,所需这样的正六边形至少为x个,至多为y个,则x+y=查看答案和解析>>
科目:初中数学 来源:2009年湖北省宜昌市夷陵中学高一数奥班选拔数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com