
【题目】如图,在矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取一点O,以点O为圆心,OF为半径作⊙O与AD相切于点P.AB=6,BC=![]()
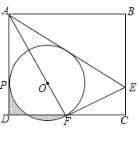
(1)求证:F是DC的中点.
(2)求证:AE=4CE.
(3)求图中阴影部分的面积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)易求DF长度即可判断;
(2)通过30°角所对的直角边等于斜边一半证得AE=2EF,EF=2CE即可得;
(3)先证明△OFG为等边三角形,△OPG为等边三角形,即可确定扇形圆心角∠POG和∠GOF的大小均为60°,所以两扇形面积相等, 通过割补法得出最后阴影面积只与矩形OPDH和△OGF有关,根据面积公式求出两图形面积即可.
(1)∵AF=AB=6,AD=BC=![]() ,
,
∴DF=3,
∴CF=DF=3,
∴F是CD的中点
(2)∵AF=6, DF=3,
∴∠DAF=30°,
∴∠EAF=30 ,
∴AE=2EF;
∴∠EFC=30 ,EF=2CE,
∴AE=4CE
(3)如图,连接OP,OG,作OH⊥FG,
∵∠AFD=60°,OF=OG,
∴△OFG为等边三角形,
同理△OPG为等边三角形,
∴∠POG=∠FOG=60°,OH=![]() ,
,
∴S扇形OPG=S扇形OGF,
∴S阴影=(S矩形OPDH-S扇形OPG-S△OGH)+(S扇形OGF-S△OFG)=S矩形OPDH-![]() S△OFG
S△OFG
=![]() ,
,
即图中阴影部分的面积![]() .
.



 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图①,在平行四边形ABCD中,对角线AC、BD交于点O,AB=AC,AB⊥AC,过点A作AE⊥BD于点E.
(1)若BC=6![]() ,求AE的长度;
,求AE的长度;
(2)如图②,点F是BD上一点,连接AF,过点A作AG⊥AF,且AG=AF,连接GC交AE于点H,证明:GH=CH.
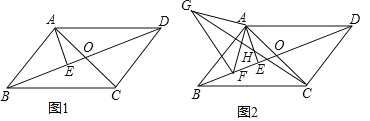
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(Ⅰ)若花园的面积是252m2,求AB的长;
(Ⅱ)当AB的长是多少时,花园面积最大?最大面积是多少?
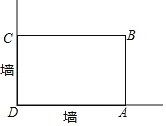
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天猫商城某网店销售童装,在春节即将将来临之际,开展了市场调查发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件;如果每件童装降价1元,那么平均每天可售出2件.
(1)假设每件童装降价![]() 元时,每天可销售 件,每件盈利 元;(用含
元时,每天可销售 件,每件盈利 元;(用含![]() 人代数式表示)
人代数式表示)
(2)每件童装降价多少元时,平均每天盈利最多?每天最多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2-4ax+4(a≠0)与y轴交于点A.过点B(0,3)作y轴的垂线l,若抛物线y=ax2-4ax+4(a≠0)与直线l有两个交点,设其中靠近y轴的交点的横坐标为m,且│m│<1,则a的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出的问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲同学的方案修改为只用2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆八中建校80周年,在体育、艺术、科技等方面各具特色,其中排球选修课是体育特色项目之一.体育组老师为了了解初一年级学生的训练情况,随机抽取了初一年级部分学生进行1分钟垫球测试,并将这些学生的测试成绩(即1分钟的垫球个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级(不包括90),90~120范围内的记为C级(不包括120),120~150范围内的记为B级(不包括150),150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:

(1)在这次测试中,一共抽取了 名学生,并补全频数分布直方图:在扇形统计图中,D级对应的圆心角的度数为 度.
(2)王攀同学在这次测试中1分钟垫球140个.他为了了解自己垫球个数在年级排名的大致情况,他把成绩为B等的全部同学1分钟垫球人数做了统计,其统计结果如表:
成绩(个) | 120 | 125 | 130 | 135 | 140 | 145 |
人数(频数) | 2 | 8 | 3 | 10 | 9 | 8 |
(垫球个数计数原则:120<垫球个数≤125记为125,125<垫球个数≤130记为130,依此类推)请你估计王攀同学的1分钟垫球个数在年级排名的大致情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com