
【题目】已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.
(1)求证:△BDE∽△CFD;
(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;
(3)当△AOF是等腰三角形时,求BE的长.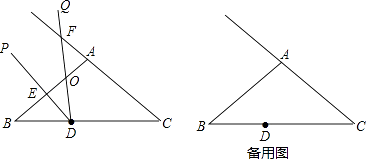
【答案】
(1)
证明:∵AB=AC,
∴∠B=∠C,
∵∠EDC=∠B+∠BED,
∴∠FDC+∠EDO=∠B+∠BED,
∵∠EDO=∠B,
∴∠BED=∠EDC,
∵∠B=∠C,
∴△BDE∽△CFD.
(2)
解:过点D作DM∥AB交AC于M(如图1中).
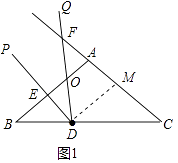
∵△BDE∽△CFD,
∴ ![]() ,∵BC=8,BD=3,BE=x,
,∵BC=8,BD=3,BE=x,
∴ ![]() =
= ![]() ,
,
∴FC= ![]() ,
,
∵DM∥AB,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DM= ![]() ,
,
∵DM∥AB,
∴∠B=∠MDC,
∴∠MDC=∠C,
∴CM=DM= ![]() ,FM=
,FM= ![]() ﹣
﹣ ![]() ,
,
∵DM∥AB,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴y= ![]() (0<x<3).
(0<x<3).
(3)
解:①当AO=AF时,
由(2)可知AO=y= ![]() ,AF=FC﹣AC=
,AF=FC﹣AC= ![]() ﹣5,
﹣5,
∴ ![]() =
= ![]() ﹣5,解得x=
﹣5,解得x= ![]() .
.
∴BE= ![]()
②当FO=FA时,易知DO=AM= ![]() ,作DH⊥AB于H(如图2中),
,作DH⊥AB于H(如图2中),
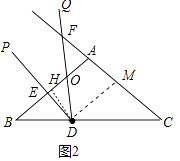
BH=BDcos∠B=3× ![]() =
= ![]() ,
,
DH=BDsin∠B=3× ![]() =
= ![]() ,
,
∴HO= ![]() =
= ![]() ,
,
∴OA=AB﹣BH﹣HO= ![]() ,
,
由(2)可知y= ![]() ,即
,即 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴BE= ![]() .
.
③当OA=OF时,设DP与CA的延长线交于点N(如图3中).
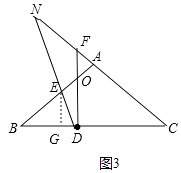
∴∠OAF=∠OFA,∠B=∠C=∠ANE,
由△ABC≌△CDN,可得CN=BC=8,ND=5,
由△BDE≌△NAE,可得NE=BE=x,ED=5﹣x,
作EG⊥BC于G,则BG= ![]() x,EG=
x,EG= ![]() x,
x,
∴GD= ![]() ,
,
∴BG+GD= ![]() x+
x+ ![]() =3,
=3,
∴x= ![]() >3(舍弃),
>3(舍弃),
综上所述,当△OAF是等腰三角形时,BE= ![]() 或
或 ![]() .
.
【解析】(1)根据两角对应相等两三角形相似即可证明.(2)过点D作DM∥AB交AC于M(如图1中).由△BDE∽△CFD,得 ![]() ,推出FC=
,推出FC= ![]() ,由DM∥AB,得
,由DM∥AB,得 ![]() ,推出DM=
,推出DM= ![]() ,由DM∥AB,推出∠B=∠MDC,∠MDC=∠C,CM=DM=
,由DM∥AB,推出∠B=∠MDC,∠MDC=∠C,CM=DM= ![]() ,FM=
,FM= ![]() ﹣
﹣ ![]() ,于DM∥AB,得
,于DM∥AB,得 ![]() ,代入化简即可.(3)分三种情形讨论①当AO=AF时,②当FO=FA时,③当OA=OF时,分别计算即可.
,代入化简即可.(3)分三种情形讨论①当AO=AF时,②当FO=FA时,③当OA=OF时,分别计算即可.
【考点精析】本题主要考查了相似三角形的判定与性质和相似三角形的应用的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题: ①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点. 
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AB中点,联结CD. 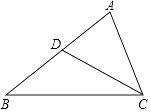
(1)若AB=10且∠ACD=∠B,求AC的长.
(2)过D点作BC的平行线交AC于点E,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,请用向量
,请用向量 ![]() 、
、 ![]() 表示
表示 ![]() 和
和 ![]() (直接写出结果)
(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设 ![]() =
= ![]() ,
, ![]() =
= ![]() .求:
.求: 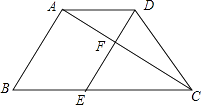
(1)向量 ![]() (用向量
(用向量 ![]() 、
、 ![]() 表示);
表示);
(2)tanB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )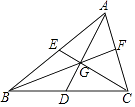
A.AC=10
B.AB=15
C.BG=10
D.BF=15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点D位于△ABC边AC上,已知AB是AD与AC的比例中项. 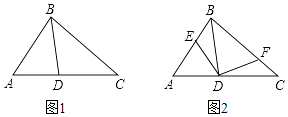
(1)求证:∠ACB=∠ABD;
(2)现有点E、F分别在边AB、BC上如图2,满足∠EDF=∠A+∠C,当AB=4,BC=5,CA=6时,求证:DE=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c的图象经过点A(m,0)、B(0,n),其中m、n是方程x2﹣6x+5=0的两个实数根,且m<n.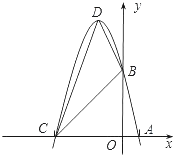
(1)求抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,求C、D点的坐标和△BCD的面积;
(3)P是线段OC上一点,过点P作PH⊥x轴,交抛物线于点H,若直线BC把△PCH分成面积相等的两部分,求P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com