
ЁОЬтФПЁПШчЭМ1ЃЌ![]() ЕФгрЧажЕЮЊ2ЃЌ
ЕФгрЧажЕЮЊ2ЃЌ![]() ЃЌЕуDЪЧЯпЖЮ
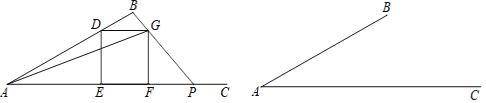
ЃЌЕуDЪЧЯпЖЮ![]() ЩЯЕФвЛЖЏЕуЃЈЕуDВЛгыЕуAЁЂBжиКЯЃЉЃЌвдЕуDЮЊЖЅЕуЕФе§ЗНаЮ
ЩЯЕФвЛЖЏЕуЃЈЕуDВЛгыЕуAЁЂBжиКЯЃЉЃЌвдЕуDЮЊЖЅЕуЕФе§ЗНаЮ![]() ЕФСэСНИіЖЅЕуEЁЂFЖМдкЩфЯп
ЕФСэСНИіЖЅЕуEЁЂFЖМдкЩфЯп![]() ЩЯЃЌЧвЕуFдкЕуEЕФгвВрЃЌСЊНс
ЩЯЃЌЧвЕуFдкЕуEЕФгвВрЃЌСЊНс![]() ЃЌВЂбгГЄ
ЃЌВЂбгГЄ![]() ЃЌНЛЩфЯп
ЃЌНЛЩфЯп![]() гкЕуPЃЎ
гкЕуPЃЎ
ЃЈ1ЃЉЕуDдкдЫЖЏЪБЃЌЯТСаЕФЯпЖЮКЭНЧжаЃЌ________ЪЧЪМжеБЃГжВЛБфЕФСПЃЈЬюађКХЃЉЃЛ
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЃЛЂо
ЃЛЂо![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩше§ЗНаЮЕФБпГЄЮЊxЃЌЯпЖЮ![]() ЕФГЄЮЊyЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђЃЛ
ЕФГЄЮЊyЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђЃЛ
ЃЈ3ЃЉШчЙћ![]() гы
гы![]() ЯрЫЦЃЌЕЋУцЛ§ВЛЯрЕШЃЌЧѓДЫЪБе§ЗНаЮЕФБпГЄЃЎ
ЯрЫЦЃЌЕЋУцЛ§ВЛЯрЕШЃЌЧѓДЫЪБе§ЗНаЮЕФБпГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂмЂнЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
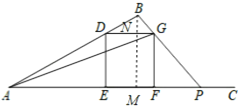
ЃЈ1ЃЉзї![]() гкMЃЌНЛ
гкMЃЌНЛ![]() гкNЃЌШчЭМЃЌРћгУШ§НЧКЏЪ§ЕФЖЈвхЕУЕН
гкNЃЌШчЭМЃЌРћгУШ§НЧКЏЪ§ЕФЖЈвхЕУЕН![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌРћгУЙДЙЩЖЈРэЕУ
ЃЌРћгУЙДЙЩЖЈРэЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ![]() ЃЌЩше§ЗНаЮЕФБпГЄЮЊxЃЌдђ
ЃЌЩше§ЗНаЮЕФБпГЄЮЊxЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌгЩгк
ЃЌгЩгк![]() ЃЌдђПЩХаЖЯ
ЃЌдђПЩХаЖЯ![]() ЮЊЖЈжЕЃЛдйРћгУ
ЮЊЖЈжЕЃЛдйРћгУ![]() ЕУЕН
ЕУЕН![]() ЃЌдђПЩХаЖЯ
ЃЌдђПЩХаЖЯ![]() ЮЊЖЈжЕЃЛдк
ЮЊЖЈжЕЃЛдк![]() жаЃЌРћгУЙДЙЩЖЈРэКЭШ§НЧКЏЪ§ПЩХаЖЯ
жаЃЌРћгУЙДЙЩЖЈРэКЭШ§НЧКЏЪ§ПЩХаЖЯ![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ![]() дкБфЛЏЃЛ
дкБфЛЏЃЛ
ЃЈ2ЃЉвзЕУЫФБпаЮ![]() ЮЊОиаЮЃЌдђ
ЮЊОиаЮЃЌдђ![]() ЃЌжЄУї
ЃЌжЄУї![]() ЃЌРћгУЯрЫЦБШПЩЕУЕНyгыxЕФЙиЯЕЪНЃЛ
ЃЌРћгУЯрЫЦБШПЩЕУЕНyгыxЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉгЩгк![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрЫЦЃЌЧвУцЛ§ВЛЯрЕШЃЌРћгУЯрЫЦБШЕУЕН
ЯрЫЦЃЌЧвУцЛ§ВЛЯрЕШЃЌРћгУЯрЫЦБШЕУЕН![]() ЃЌЬжТлЃКЕБЕуPдкЕуFЕугвВрЪБЃЌдђ
ЃЌЬжТлЃКЕБЕуPдкЕуFЕугвВрЪБЃЌдђ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌЕБЕуPдкЕуFЕузѓВрЪБЃЌдђ
ЃЌЕБЕуPдкЕуFЕузѓВрЪБЃЌдђ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌШЛКѓЗжБ№НтЗНГЬМДПЩЕУЕНе§ЗНаЮЕФБпГЄЃЎ
ЃЌШЛКѓЗжБ№НтЗНГЬМДПЩЕУЕНе§ЗНаЮЕФБпГЄЃЎ
ЃЈ1ЃЉШчЭМЃЌзї![]() гкMЃЌНЛ
гкMЃЌНЛ![]() гкNЃЌ
гкNЃЌ
дк![]() жаЃЌЁп
жаЃЌЁп![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Щше§ЗНаЮЕФБпГЄЮЊxЃЌ
дк![]() жаЃЌЁп
жаЃЌЁп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
Жј![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ
Ёр![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ
Ёр![]() дкБфЛЏЃЌ
дкБфЛЏЃЌ
Ыљвд![]() КЭ
КЭ![]() ЪЧЪМжеБЃГжВЛБфЕФСПЃЛ
ЪЧЪМжеБЃГжВЛБфЕФСПЃЛ
ЙЪД№АИЮЊЃКЂмЂн
ЃЈ2ЃЉЁпMNЁЭAPЃЌDEFGЪЧе§ЗНаЮЃЌ
ЁрЫФБпаЮ![]() ЮЊОиаЮЃЌ
ЮЊОиаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
Ёр![]()
ЃЈ3ЃЉЁп![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрЫЦЃЌЧвУцЛ§ВЛЯрЕШЃЌ
ЯрЫЦЃЌЧвУцЛ§ВЛЯрЕШЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБЕуPдкЕуFЕугвВрЪБЃЌAP=AF+PF=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЕБЕуPдкЕуFЕузѓВрЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ

злЩЯЫљЪіЃЌе§ЗНаЮЕФБпГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдЪЕЪ§aЃЌbЃЌЖЈвхдЫЫуЁА*ЁБЮЊЃКa*bЃН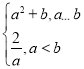
ЃЈ1ЃЉЧѓКЏЪ§yЃНx*ЃЈ2xЉ1ЃЉЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуAЃЈx1ЃЌy1ЃЉЁЂBЃЈx2ЃЌy2ЃЉЃЈx1ЃМx2ЃЉдкКЏЪ§yЃНx*ЃЈ2xЉ1ЃЉЕФЭМЯѓЩЯЃЌЧвAЁЂBСНЕуЙигкзјБъдЕуГЩжааФЖдГЦЃЌЧѓЕуAЕФзјБъЃЛ
ЃЈ3ЃЉЙигкxЕФЗНГЬx*ЃЈ2xЉ1ЃЉЃНmЧЁгаШ§ИіЛЅВЛЯрЕШЕФЪЕЪ§Иљx1ЃЌx2ЃЌx3ЃЌЧвx1ЃМx2ЃМx3ЃЌЩшtЃНx1+2x2+x3+x1x2x3ЃЌдђtЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
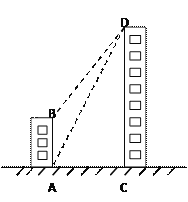
ЁОЬтФПЁПШчЭМЃЌвЛЖАОгУёТЅABЕФИпЮЊ16УзЃЌдЖДІгавЛЖАЩЬЮёТЅCDЃЌаЁУїдкОгУёТЅЕФТЅЕзAДІВтЕУЩЬЮёТЅЖЅDДІЕФбіНЧЮЊ![]() ЃЌгждкЩЬЮёТЅЕФТЅЖЅDДІВтЕУОгУёТЅЕФТЅЖЅBДІЕФИЉНЧЮЊ
ЃЌгждкЩЬЮёТЅЕФТЅЖЅDДІВтЕУОгУёТЅЕФТЅЖЅBДІЕФИЉНЧЮЊ![]() ЃЎЦфжаAЁЂCСНЕуЗжБ№ЮЛгкBЁЂDСНЕуЕФе§ЯТЗНЃЌЧвAЁЂCСНЕудкЭЌвЛЫЎЦНЯпЩЯЃЌЧѓЩЬЮёТЅCDЕФИпЖШЃЎ
ЃЎЦфжаAЁЂCСНЕуЗжБ№ЮЛгкBЁЂDСНЕуЕФе§ЯТЗНЃЌЧвAЁЂCСНЕудкЭЌвЛЫЎЦНЯпЩЯЃЌЧѓЩЬЮёТЅCDЕФИпЖШЃЎ
(ВЮПМЪ§ОнЃК ![]() ЃЌ
ЃЌ ![]() .НсЙћОЋШЗЕН0.1Уз)
.НсЙћОЋШЗЕН0.1Уз)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ10ЗжЃЉЫЎЙћЕъеХАЂвЬвдУПНя2дЊЕФМлИёЙКНјФГжжЫЎЙћШєИЩНяЃЌШЛКѓвдУПНя4дЊЕФМлИёГіЪлЃЌУПЬьПЩЪлГі100НяЃЌЭЈЙ§ЕїВщЗЂЯжЃЌетжжЫЎЙћУПНяЕФЪлМлУПНЕЕЭ0.1дЊЃЌУПЬьПЩЖрЪлГі20НяЃЌЮЊБЃжЄУПЬьжСЩйЪлГі260НяЃЌеХАЂвЬОіЖЈНЕМлЯњЪлЃЎ
ЃЈ1ЃЉШєНЋетжжЫЎЙћУПНяЕФЪлМлНЕЕЭxдЊЃЌдђУПЬьЕФЯњЪлСПЪЧ НяЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉЯњЪлетжжЫЎЙћвЊЯыУПЬьгЏРћ300дЊЃЌеХАЂвЬашНЋУПНяЕФЪлМлНЕЕЭЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЩфЯп
ЮЊЩфЯп![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() ЦНЗж
ЦНЗж![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЈВЛгыЖЫЕу
ЃЈВЛгыЖЫЕу![]() ЃЌ
ЃЌ![]() жиКЯЃЉ.
жиКЯЃЉ.

ЃЈ1ЃЉЕБ![]() ЮЊШёНЧЃЌЧв
ЮЊШёНЧЃЌЧв![]() ЪБЃЌЧѓЫФБпаЮ
ЪБЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕБ![]() гы
гы![]() ЯрЫЦЪБЃЌЧѓЯпЖЮ
ЯрЫЦЪБЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђ.
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЖЈвхгђ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїРћгУКЏЪ§гыВЛЕШЪНЕФЙиЯЕЃЌЖдаЮШч![]() (
(![]() ЮЊе§ећЪ§)ЕФВЛЕШЪНЕФНтЗЈНјааСЫЬНОП.
ЮЊе§ећЪ§)ЕФВЛЕШЪНЕФНтЗЈНјааСЫЬНОП.
(1)ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећ:
ЂйЖдгкВЛЕШЪН![]() ЃЌЙлВьКЏЪ§
ЃЌЙлВьКЏЪ§![]() ЕФЭМЯѓПЩвдЕУЕНШчЯТБэИё:
ЕФЭМЯѓПЩвдЕУЕНШчЯТБэИё:
|
|
|
|
|
|
гЩБэИёПЩжЊВЛЕШЪН![]() ЕФНтМЏЮЊ
ЕФНтМЏЮЊ![]() .
.
ЂкЖдгкВЛЕШЪН![]() ЃЌЙлВьКЏЪ§
ЃЌЙлВьКЏЪ§![]() ЕФЭМЯѓПЩЕУЕНШчЯТБэИё:
ЕФЭМЯѓПЩЕУЕНШчЯТБэИё:
|
|
|
|
|
|
|
|
гЩБэИёПЩжЊВЛЕШЪН![]() ЕФНтМЏЮЊ .
ЕФНтМЏЮЊ .
ЂлЖдгкВЛЕШЪН![]() ,ЧыИљОнвбУшГіЕФЕуЛГіКЏЪ§
,ЧыИљОнвбУшГіЕФЕуЛГіКЏЪ§![]() ЕФЭМЯѓ;
ЕФЭМЯѓ;
ЙлВьКЏЪ§![]() ЕФЭМЯѓ,
ЕФЭМЯѓ,
ВЙШЋЯТУцЕФБэИё:
|
|
|
|
|
|
|
|
гЩБэИёПЩжЊВЛЕШЪН![]() ЕФНтМЏЮЊ .
ЕФНтМЏЮЊ .
аЁУїНЋЩЯЪіЬНОПЙ§ГЬзмНсШчЯТ:ЖдгкНтаЮШч![]() (
(![]() ЮЊе§ећЪ§)ЕФВЛЕШЪНЃЌЯШНЋ
ЮЊе§ећЪ§)ЕФВЛЕШЪНЃЌЯШНЋ![]() АДДгДѓЕНаЁЕФЫГађХХСаЃЌдйЛЎЗж
АДДгДѓЕНаЁЕФЫГађХХСаЃЌдйЛЎЗж![]() ЕФЗЖЮЇЃЌШЛКѓЭЈЙ§СаБэИёЕФАьЗЈЃЌПЩвдЗЂЯжБэИёжа
ЕФЗЖЮЇЃЌШЛКѓЭЈЙ§СаБэИёЕФАьЗЈЃЌПЩвдЗЂЯжБэИёжа![]() ЕФЗћКХГЪЯжвЛЖЈЕФЙцТЩЃЌРћгУетИіЙцТЩПЩвдЧѓетбљЕФВЛЕШЪНЕФНтМЏ.
ЕФЗћКХГЪЯжвЛЖЈЕФЙцТЩЃЌРћгУетИіЙцТЩПЩвдЧѓетбљЕФВЛЕШЪНЕФНтМЏ.
(2)ЧыФуВЮПМаЁУїЕФЗНЗЈЃЌНтОіЯТСаЮЪЬт:
ЂйВЛЕШЪН![]() ЕФНтМЏЮЊ .
ЕФНтМЏЮЊ .
ЂкВЛЕШЪН![]() ЕФНтМЏЮЊ .
ЕФНтМЏЮЊ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЈШчЭМЃЉЃЌЕу
ЃЈШчЭМЃЉЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊЩфЯп
ЗжБ№ЮЊЩфЯп![]() ЩЯЕФЖЏЕуЃЈЕуCЁЂEЖМВЛгыЕуBжиКЯЃЉЃЌСЌНгACЁЂAEЪЙЕУ
ЩЯЕФЖЏЕуЃЈЕуCЁЂEЖМВЛгыЕуBжиКЯЃЉЃЌСЌНгACЁЂAEЪЙЕУ![]() ЃЌЩфЯп
ЃЌЩфЯп![]() НЛЩфЯп
НЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() .
.
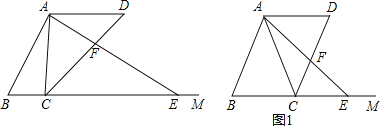
ЃЈ1ЃЉШчЭМ1ЃЌЕБ![]() ЪБЃЌЧѓAFЕФГЄ.
ЪБЃЌЧѓAFЕФГЄ.
ЃЈ2ЃЉЕБЕу![]() дкЕу
дкЕу![]() ЕФгвВрЪБЃЌЧѓ
ЕФгвВрЪБЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіКЏЪ§ЕФЖЈвхгђ.
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіКЏЪ§ЕФЖЈвхгђ.
ЃЈ3ЃЉСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЪЧЕШбќШ§НЧаЮЃЌжБНгаДГі
ЪЧЕШбќШ§НЧаЮЃЌжБНгаДГі![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
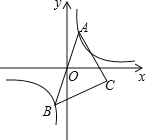
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЪЧЫЋЧњЯпyЃН![]() дкЕквЛЯѓЯоЕФЗжжЇЩЯЕФвЛИіЖЏЕуЃЌСЌНсAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќжБНЧЁїABCЃЌЕуCдкЕкЫФЯѓЯоЃЎЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯБфЛЏЃЌЕЋЕуCЪМжедкЫЋЧњЯпyЃН
дкЕквЛЯѓЯоЕФЗжжЇЩЯЕФвЛИіЖЏЕуЃЌСЌНсAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќжБНЧЁїABCЃЌЕуCдкЕкЫФЯѓЯоЃЎЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯБфЛЏЃЌЕЋЕуCЪМжедкЫЋЧњЯпyЃН![]() ЃЈkЃМ0ЃЉЩЯдЫЖЏЃЌдђkЕФжЕЪЧ_____ЃЎ
ЃЈkЃМ0ЃЉЩЯдЫЖЏЃЌдђkЕФжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЩюЛЏПЮИФЃЌТфЪЕСЂЕТЪїШЫФПБъЃЌФГбЇаЃЩшжУСЫвдЯТЫФУХЭиеЙадПЮГЬЃКAЃЎЪ§бЇЫМЮЌЃЌBЃЎЮФбЇМјЩЭЃЌCЃЎКьДЌПЮГЬЃЌDЃЎ3DДђгЁЃЌЙцЖЈУПЮЛбЇЩњбЁБЈвЛУХЃЎЮЊСЫНтбЇЩњЕФБЈУћЧщПіЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌВЂжЦзїГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыЛиД№ЯТСаЮЪЬтЃК
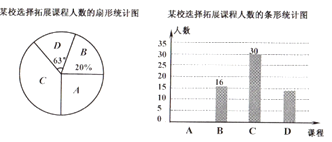
ЃЈ1ЃЉЧѓетДЮБЛЕїВщЕФбЇЩњШЫЪ§ЃЛ
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉМйШчШЋаЃгабЇЩњ1000ШЫЃЌЧыЙРМЦбЁБЈЁАКьДЌПЮГЬЁБЕФбЇЩњШЫЪ§.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com