
【题目】如图1,在平面直角坐标系中,已知![]() 的半径为5,圆心
的半径为5,圆心![]() 的坐标为
的坐标为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是
是![]() 上的一点(不与点
上的一点(不与点![]() 、
、![]() 、
、![]() 重合),连结
重合),连结![]() 并延长,连结
并延长,连结![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)当点![]() 在
在![]() 上时.
上时.
①求证:![]() ;
;
②如图2,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连结
,连结![]() .求证:
.求证:![]() ;
;
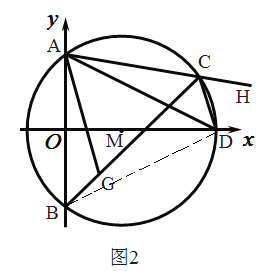
(3)如图3,当点![]() 在
在![]() 上运动的过程中,试探究
上运动的过程中,试探究![]() 的值是否发生变化?若不变,请直接写出该定值;若变化,请说明理由.
的值是否发生变化?若不变,请直接写出该定值;若变化,请说明理由.
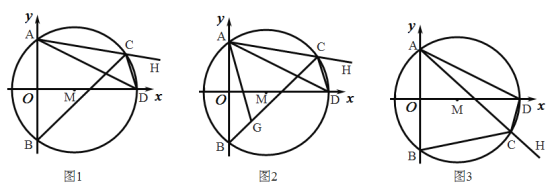
【答案】(1)(0,4);(2)①详见解析;②详见解析;(3)不变,为![]() .
.
【解析】
(1)连结![]() ,在
,在![]() 中,
中,![]() 为圆的半径5,
为圆的半径5,![]() ,由勾股定理得
,由勾股定理得![]()
(2)①根据圆的基本性质及圆周角定理即可证明;
②根据等腰三角形的性质得到![]() ,根据三角形的外角定理得到
,根据三角形的外角定理得到![]() ,由①证明
,由①证明![]() 得到
得到![]() ,即可根据相似三角形的判定进行求解;
,即可根据相似三角形的判定进行求解;
(3)分别求出点C在B点时和点C为直径AC时,![]() 的值,即可比较求解.
的值,即可比较求解.
(1)连结![]() ,在
,在![]() 中,
中,![]() =5,
=5,![]() ,
,
∴![]()
∴A(0,4).
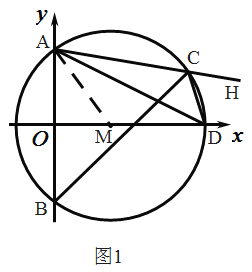
(2)连结![]() ,
,![]()
故![]() ,则
,则![]()
∵∠ABD+∠ACD=180°,∠HCD+∠ACD=180°,
∴![]()
∵![]() 与
与![]() 是弧
是弧![]() 所对的圆周角
所对的圆周角
∴![]() =
=![]()
又![]()
∴![]()
即![]()
②∵![]()
∴![]()
∵![]() ,且由(2)得
,且由(2)得![]()
∴![]()
∴![]()
在![]() 与
与![]() 中
中
![]()
∴![]()
(3)①点C在B点时,如图,
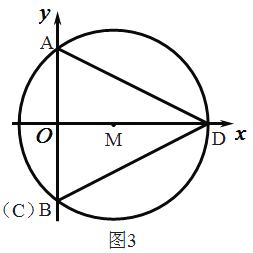
AC=2AO=8,BC=0,
CD=BD=![]()
∴![]() =
=![]() =
=![]() ;
;
当点C为直径AC与圆的交点时,如图
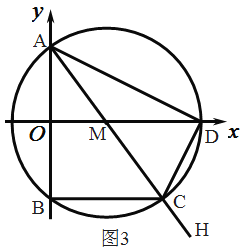
∴AC=2r=10
∵O,M分别是AB、AC中点,
∴BC=2OM=6,
∴C(6,-4)∵D(8,0)
∴CD=![]()
∴![]() =
=![]() =
=![]()
故![]() 的值不变,为
的值不变,为![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,AC为圆O的直径,弦AD的延长线与过点C的切线交于点B,E为BC中点,AC= ![]() ,BC=4.
,BC=4.
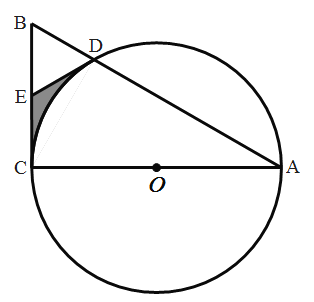
(1)求证:DE为圆O的切线;
(2)求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
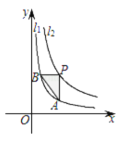
【题目】如图,函数![]() (x>0)和
(x>0)和![]() (x>0)的图象分别是
(x>0)的图象分别是![]() 和
和![]() .设点P在
.设点P在![]() 上,PA∥y轴交
上,PA∥y轴交![]() 于点A,PB∥x轴,交
于点A,PB∥x轴,交![]() 于点B,△PAB的面积为( )
于点B,△PAB的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P为⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有点A、B(不与P、Q重合),连接AP、BP,若∠APQ=∠BPQ
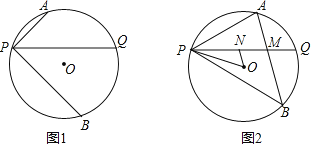
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径。
时,求⊙O的半径。
(2)如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,设∠NOP=α,∠OPN=β,若AB平行于ON,探究α与β的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与
的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,经过点
,经过点![]() 的一次函数
的一次函数![]() 的图象与
的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,且与抛物线的另一个交点为
,且与抛物线的另一个交点为![]() ,
,![]() 的面积为5.
的面积为5.
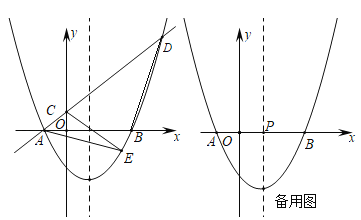
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点![]() 在一次函数的图象下方,求
在一次函数的图象下方,求![]() 面积的最大值,并求出此时点E的坐标;
面积的最大值,并求出此时点E的坐标;
(3)若点![]() 为
为![]() 轴上任意一点,在(2)的结论下,求
轴上任意一点,在(2)的结论下,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是二次函数
是二次函数![]() 图像上的任意一点,点
图像上的任意一点,点![]() 在
在![]() 轴上.
轴上.
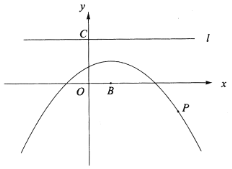
(1)以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() .
.
①直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,判断
轴平行,判断![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
②若![]() 与
与![]() 轴相切,求出点
轴相切,求出点![]() 坐标;
坐标;
(2)![]() 、
、![]() 、
、![]() 是这条抛物线上的三点,若线段
是这条抛物线上的三点,若线段![]() 、
、![]() 、
、![]() 的长满足
的长满足![]() ,则称
,则称![]() 是
是![]() 、
、![]() 的和谐点,记做
的和谐点,记做![]() .已知
.已知![]() 、
、![]() 的横坐标分别是
的横坐标分别是![]() ,
,![]() ,直接写出
,直接写出![]() 的坐标_______.
的坐标_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,DB⊥MN于点B.

(1)如图,求证:BD+AB=![]() BC;
BC;
(2)直线MN绕点A旋转,在旋转过程中,当∠BCD=30°,BD=![]() 时,求BC的值.
时,求BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,![]() 六个小朋友围成一圈(面向圈内)做传球游戏,规定:球不得传给自己,也不得传给左手边的人.若游戏中传球和接球都没有失误.
六个小朋友围成一圈(面向圈内)做传球游戏,规定:球不得传给自己,也不得传给左手边的人.若游戏中传球和接球都没有失误.
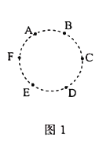
![]() 若由
若由![]() 开始一次传球,则
开始一次传球,则![]() 和
和![]() 接到球的概率分别是 、 ;
接到球的概率分别是 、 ;
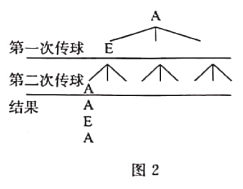
![]() 若增加限制条件:“也不得传给右手边的人”.现在球已传到
若增加限制条件:“也不得传给右手边的人”.现在球已传到![]() 手上,在下面的树状图2中
手上,在下面的树状图2中
画出两次传球的全部可能情况,并求出球又传到![]() 手上的概率.
手上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
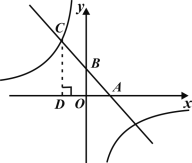
【题目】如图,已知一次函数y=ax+b(a,b为常数,a≠0)的图象与x轴,y轴分别交于点A,B,且与反比例函数![]() (k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于D,若OA=OD=
(k为常数,k≠0)的图象在第二象限内交于点C,作CD⊥x轴于D,若OA=OD=![]() OB=3.
OB=3.
(1)求一次函数与反比例函数的解析式;
(2)观察图象直接写出不等式0<ax+b≤![]() 的解集;
的解集;
(3)在y轴上是否存在点P,使得△PBC是以BC为一腰的等腰三角形?如果存在,请直接写出P点的坐标;如果不存在,请简要说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com