
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点
两点![]() 在
在![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
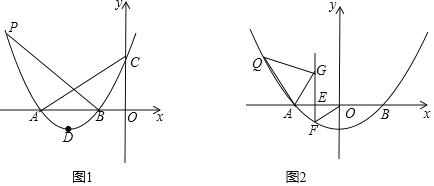
(1)当![]() 时,求四边形
时,求四边形![]() 的面积
的面积![]() ;
;
(2)在(1)的条件下,在第二象限抛物线对称轴左侧上存在一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,将(1)中抛物线沿直线![]() 向斜上方向平移
向斜上方向平移![]() 个单位时,点
个单位时,点![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 轴交新抛物线于点
轴交新抛物线于点![]() ,延长
,延长![]() 至
至![]() ,且
,且![]() ,若
,若![]() 的外角平分线交点
的外角平分线交点![]() 在新抛物线上,求
在新抛物线上,求![]() 点坐标.
点坐标.
【答案】(1)4;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)过点D作DE⊥x轴于点E,求出二次函数的顶点D的坐标,然后求出A、B、C的坐标,然后根据![]() 即可得出结论;
即可得出结论;
(2)设点![]() 是第二象限抛物线对称轴左侧上一点,将
是第二象限抛物线对称轴左侧上一点,将![]() 沿
沿![]() 轴翻折得到
轴翻折得到![]() ,点
,点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,证出
,证出![]() ,列表比例式,并找出关于t的方程即可得出结论;
,列表比例式,并找出关于t的方程即可得出结论;
(3)判断点D在直线![]() 上,根据勾股定理求出DH,即可求出平移后的二次函数解析式,设点
上,根据勾股定理求出DH,即可求出平移后的二次函数解析式,设点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 轴于
轴于![]() ,根据勾股定理求出AG,联立方程即可求出m、n,从而求出结论.
,根据勾股定理求出AG,联立方程即可求出m、n,从而求出结论.
解:(1)过点D作DE⊥x轴于点E
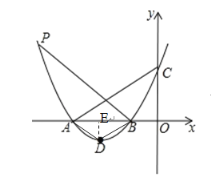
当![]() 时,得到
时,得到![]() ,
,
![]() 顶点
顶点![]() ,
,
∴DE=1
由![]() ,得
,得![]() ,
,![]() ;
;
令![]() ,得
,得![]() ;
;
![]() ,
,![]() ,
,![]() ,
,
![]() ,OC=3
,OC=3
![]() .
.
(2)如图1,设点![]() 是第二象限抛物线对称轴左侧上一点,将
是第二象限抛物线对称轴左侧上一点,将![]() 沿
沿![]() 轴翻折得到
轴翻折得到![]() ,点
,点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,
,
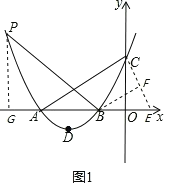
由翻折得:![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() 轴,
轴,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
由勾股定理得:![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
解得:![]() (不符合题意,舍去),
(不符合题意,舍去),![]() ;
;
![]() ,
,![]() .
.
(3)原抛物线![]() 的顶点
的顶点![]() 在直线
在直线![]() 上,
上,
直线![]() 交
交![]() 轴于点
轴于点![]() ,
,
如图2,过点![]() 作
作![]() 轴于
轴于![]() ,
,
![]() ;
;
![]() 由题意,平移后的新抛物线顶点为
由题意,平移后的新抛物线顶点为![]() ,解析式为
,解析式为![]() ,
,
设点![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 轴于
轴于![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
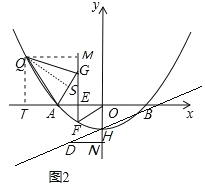
![]() 、
、![]() 分别平分
分别平分![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]() ,
,
根据题意得: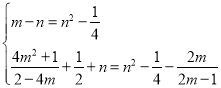
解得: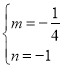
![]()


科目:初中数学 来源: 题型:
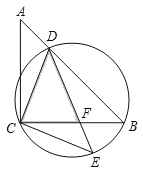
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D是AB边上的一点,连结CD,过点C作CD的垂线,与经过点C、D、B的圆交于点E,连结DE,交CB于点F.若AD=1,DB=3,则线段DE的长为_____;△CDF的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
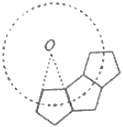
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k≠0,x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,E(
(k≠0,x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,E(![]() ,6),且E为BC的中点,D为x轴负半轴上的点.
,6),且E为BC的中点,D为x轴负半轴上的点.
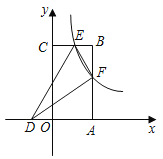
(1)求反比倒函数的表达式和点F的坐标;
(2)若D(﹣![]() ,0),连接DE、DF、EF,则△DEF的面积是 .
,0),连接DE、DF、EF,则△DEF的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉二中广雅中学为了进一步改进本校九年级数学教学,提高学生学习数学的兴趣.校教务处在九年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查:我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“![]() 非常喜欢”、“
非常喜欢”、“ ![]() 比较喜欢”、“
比较喜欢”、“ ![]() 不太喜欢”、“
不太喜欢”、“ ![]() 很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计.现将统计结果绘制成如下两幅不完整的统计图.
很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计.现将统计结果绘制成如下两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是 ,图②中![]() 所在扇形对应的圆心角是 ;
所在扇形对应的圆心角是 ;
(3)若该校九年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
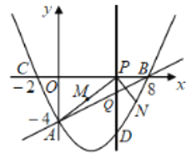
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 过点
过点![]() ,动点P在线段
,动点P在线段![]() 上以每秒2个单位长度的速度由点
上以每秒2个单位长度的速度由点![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() , 交抛物线于点
, 交抛物线于点![]() .连接
.连接![]() ,
,![]() 是线段
是线段![]() 的中点,将线段
的中点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() .
.
(1)求抛物线的解析式;
(2)连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 面积有最大值,最大值是多少?
面积有最大值,最大值是多少?
(3)当![]() 为何值时,点
为何值时,点![]() 落在抛物线上.
落在抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连接CF并延长交AB于点M,MN⊥CM交射线AD于点N
(1)如图1,当点F为BE的中点时,求证:AM=CE;
(2)如图2,若![]() =
=![]() =n(n≥3)时,请直接写出
=n(n≥3)时,请直接写出![]() 的值;
的值;
(3)若矩形ABCD(AB>BC)对角线AC交MN于T,H为边BC上一点,∠CMH=45°且![]() =
=![]() (如图3).若CF平分∠ACB,请直接写出
(如图3).若CF平分∠ACB,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.

运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | b | 7 | 5 | 8 | a | 8 | 7 |
(1)若运动员丙测试成绩的平均数和众数都是7,则成绩表中的a= ,b= ;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为S甲2=0.81、S乙2=0.4、S丙2=0.8)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,第二轮结束时球又回到乙手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成(1)~(3)题:
数学课上,老师出示了这样一道题:
如图1,△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,E是AC的中点,经过点A、C作射线BE的垂线,垂足分别为点F、G,连接AG.探究线段DF和AG的关系.某学习小组的同学经过思考后,交流了自己的想法:
小明:“经过观察和度量,发现∠ABF和∠ACG相等.”小刚:“经过观察和度量,发现有两条线段和AF相等.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段DF和AG的关系.”
……
老师:“若点E不是AC的中点,其他条件不变(如图2),可以求出![]() 的值.”
的值.”
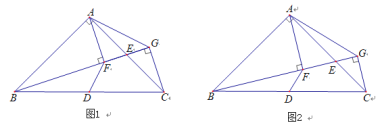
(1)求证:AF=FG;
(2)探究线段DF和AG的关系,并证明;
(3)直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com