
 9、如图,点A在射线OB上,OA的长为2cm.如果OA绕点O按逆时针方向旋转30°到OA',那么点A'的位置可以用(2,30°)表示.按上述表示方法,如果将OA'再绕点O按逆时针方向继续旋转25°到OA″,那么点A″的位置可以用(
9、如图,点A在射线OB上,OA的长为2cm.如果OA绕点O按逆时针方向旋转30°到OA',那么点A'的位置可以用(2,30°)表示.按上述表示方法,如果将OA'再绕点O按逆时针方向继续旋转25°到OA″,那么点A″的位置可以用(
科目:初中数学 来源: 题型:
 如图,点A在射线OP上,OA等于2cm.我们定义如下两种操作
如图,点A在射线OP上,OA等于2cm.我们定义如下两种操作查看答案和解析>>
科目:初中数学 来源: 题型:填空题
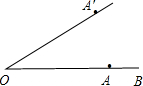 如图,点A在射线OB上,OA的长为2cm.如果OA绕点O按逆时针方向旋转30°到OA',那么点A'的位置可以用(2,30°)表示.按上述表示方法,如果将OA'再绕点O按逆时针方向继续旋转25°到OA″,那么点A″的位置可以用(________,________ )表示.
如图,点A在射线OB上,OA的长为2cm.如果OA绕点O按逆时针方向旋转30°到OA',那么点A'的位置可以用(2,30°)表示.按上述表示方法,如果将OA'再绕点O按逆时针方向继续旋转25°到OA″,那么点A″的位置可以用(________,________ )表示.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点A在射线OP上,OA等于2cm.我们定义如下两种操作:
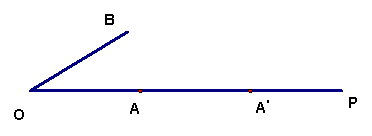
操作一 ![]() 旋转操作,记为X操作:
旋转操作,记为X操作:
OA绕点O按逆时针方向旋转![]() 到OB,那么点B的位置可以用(2,
到OB,那么点B的位置可以用(2,![]() )表示;OB绕点O再按逆时针方向旋转
)表示;OB绕点O再按逆时针方向旋转![]() 到OC,那么点C的位置可以用(2,
到OC,那么点C的位置可以用(2,![]() )表示.
)表示.
操作二 线段加倍操作,记为Y操作:
如图,如果延长OA到点![]() ,使
,使![]() =2
=2![]() ,那么点
,那么点![]() 的位置可以用(4,
的位置可以用(4,![]() )表示;如果延长OB到点
)表示;如果延长OB到点![]() ,使
,使![]() =2
=2![]() ,那么点
,那么点![]() 的位置可以用(4,
的位置可以用(4,![]() )表示.
)表示.
(1)现操作如下:
第一次对点A进行X操作,得到第一个点![]() ,其位置可以表示为( ,
,其位置可以表示为( , ![]() );
);
第二次对点![]() 进行Y操作,得到第二个点
进行Y操作,得到第二个点![]() ,其位置可以表示为( ,
,其位置可以表示为( , ![]() );
);
第三次对点![]() 进行X操作,得到第三个点
进行X操作,得到第三个点![]() ,其位置可以表示为( ,
,其位置可以表示为( , ![]() );
);
第四次对点![]() 进行Y操作,得到第四个点
进行Y操作,得到第四个点![]() ,其位置可以表示为( ,
,其位置可以表示为( , ![]() );
);
……,如此依次进行操作X、Y、X、Y、![]() ,可得到若干点.
,可得到若干点.
(2)按如上操作,若经过t次操作后得到A2010点,其位置表示为(p,q![]() ),则t、p、q的值分别为多少?
),则t、p、q的值分别为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com