
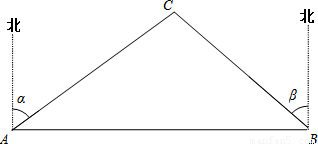
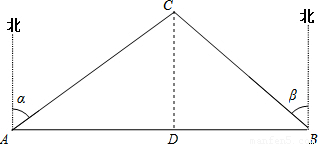
 解:AB不穿过风景区.理由如下:
解:AB不穿过风景区.理由如下: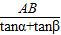 =
=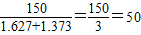 (千米).
(千米).

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖北荆门卷)数学(解析版) 题型:解答题
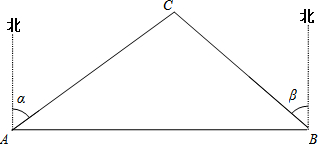
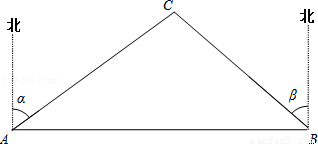
A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
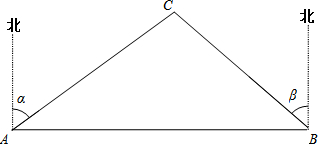
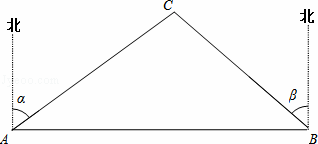
A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com