
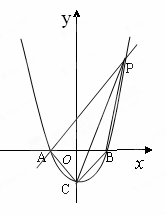
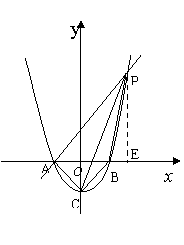
如图,已知抛物线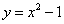 与
与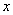 轴交于A、B两点,与
轴交于A、B两点,与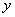 轴交于点C.
轴交于点C.
(1)求A、B、C三点的坐标.
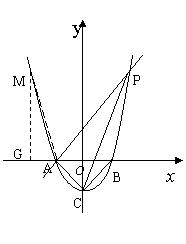
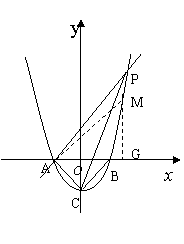
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
(3)在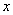 轴上方的抛物线上是否存在一点M,过M作MG
轴上方的抛物线上是否存在一点M,过M作MG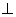
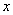 轴于点G,使以A、M、G三点为顶点的三角形与
轴于点G,使以A、M、G三点为顶点的三角形与 PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
解:(1)令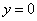 ,得
,得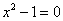 解得
解得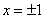
令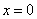 ,得
,得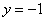
∴ A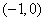 B
B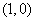 C
C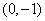
(2)∵OA=OB=OC=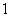 ∴
∴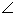 BAC=
BAC=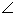 ACO=
ACO=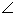 BCO=
BCO=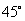
∵AP∥CB, ∴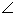 PAB=
PAB=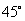
过点P作PE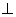
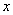 轴于E,则
轴于E,则 APE为等腰直角三角形
APE为等腰直角三角形
令OE=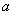 ,则PE=
,则PE=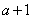 ∴P
∴P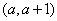
∵点P在抛物线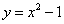 上 ∴
上 ∴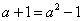
解得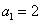 ,
,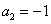 (不合题意,舍去)
(不合题意,舍去)
∴PE=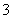
∴四边形ACBP的面积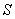 =
=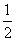 AB•OC+
AB•OC+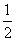 AB•PE
AB•PE
=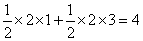
(3). 假设存在
∵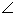 PAB=
PAB=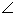 BAC =
BAC =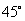 ∴PA
∴PA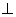 AC
AC
∵MG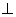
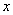 轴于点G,
轴于点G, ∴
∴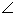 MGA=
MGA=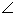 PAC =
PAC =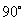
在Rt△AOC中,OA=OC=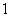 ∴AC=
∴AC=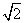
在Rt△PAE中,AE=PE=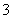 ∴AP=
∴AP= 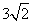
设M点的横坐标为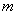 ,则M
,则M 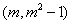
 ①点M在
①点M在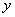 轴左侧时,则
轴左侧时,则
(ⅰ) 当 AMG
AMG 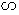
 PCA时,有
PCA时,有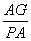 =
=
∵AG=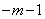 ,MG=
,MG=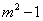
即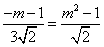
 解得
解得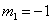 (舍去)
(舍去) 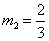 (舍去)
(舍去)
(ⅱ) 当 MA
MA G
G 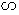
 PCA时有
PCA时有 =
=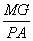
即 
解得:
 (舍去)
(舍去) 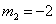
∴M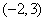
② 点M在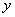 轴右侧时,则
轴右侧时,则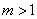
(ⅰ) 当 AMG
AMG 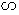
 PC
PC A时有
A时有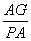 =
=
∵AG=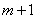 ,MG=
,MG=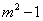
∴ 
解得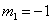 (舍去)
(舍去) 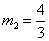
∴M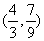


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
图①、图②都是4×4的正方形网格,小正方形的边长均为1,每个小正方形的
顶点称为格点.在①、②两个网格中分别标注了5个格点,按下列要求画图:
(1)在图①中以格点为顶点,画一个等腰三角形,使其内部含有已标注的3个格点;
(2)在图②中以格点为顶点,画一个正方形,使其边长为无理数,并使其内部含有已
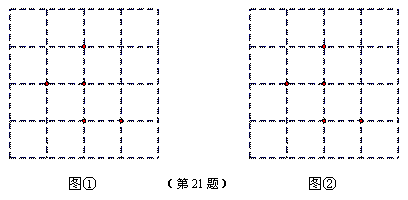 标注的3个格点.
标注的3个格点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com