
 将下面证明中每一步的理由写在横线上:
将下面证明中每一步的理由写在横线上:

科目:初中数学 来源: 题型:
 请将下面证明中每一步的理由填在括号内:
请将下面证明中每一步的理由填在括号内:| 1 |
| 2 |
| 1 |
| 2 |
| 180°-120° |
| 2 |
查看答案和解析>>
科目:初中数学 来源:新课标3维同步训练与评价·数学·九年级·上 题型:044
将下面证明中每一步的理由写在括号内.
已知:如下图,AB=AC、DB=DC、AD的延长线交BC于E.
求证:AE⊥BC

证明:在△ABD和△ACD中
∵AB=AC( )
DB=DC( )
AD=AD( )
∴△ABD≌△ACD( )
∴∠BAD=∠CAD( )
即AE为∠BAC平分线
∴AE⊥BC( )
查看答案和解析>>
科目:初中数学 来源: 题型:044
将下面证明中每一步的理由写在括号内:
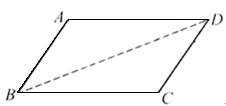
已知:如图,AB=CD,AD=CB.
求证:∠A=∠C.
证明:连接BD.
在△BAD和△DCB中,
∵AB=CD( )
AD=CB( )
BD=DB( )
∴△BAD≌△DCB( )
∴∠A=∠C( )
查看答案和解析>>
科目:初中数学 来源:2011-2012学年贵州省毕节地区织金六中九年级(上)期中数学试卷(解析版) 题型:解答题
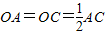 ,
,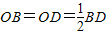 ______
______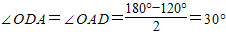 .______
.______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com