
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图所示,根据题中相关信息回答下列问题: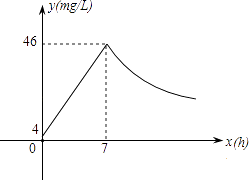
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
【答案】
(1)解:因为爆炸前浓度呈直线型增加,
所以可设y与x的函数关系式为y=k1x+b(k1≠0),
由图象知y=k1x+b过点(0,4)与(7,46),
则 ![]() ,
,
解得 ![]() ,
,
则y=6x+4,此时自变量x的取值范围是0≤x≤7.
∵爆炸后浓度成反比例下降,
∴可设y与x的函数关系式为 ![]() (k2≠0).
(k2≠0).
由图象知 ![]() 过点(7,46),
过点(7,46),
∴ ![]() ,
,
∴k2=322,
∴ ![]() ,此时自变量x的取值范围是x>7.
,此时自变量x的取值范围是x>7.
(2)解:当y=34时,由y=6x+4得,6x+4=34,x=5.
∴撤离的最长时间为7﹣5=2(小时).
∴撤离的最小速度为3÷2=1.5(km/h).
(3)解:当y=4时,由y= ![]() 得,x=80.5,
得,x=80.5,
80.5﹣7=73.5(小时).
∴矿工至少在爆炸后73.5小时才能下井.
【解析】(1)因为爆炸前浓度呈直线型增加,所以可知是一次函数,可设y与x的函数关系式为y=k1x+b(k1≠0),由图象过点求出k1=6,b=4, 则y=6x+4,此时自变量x的取值范围是0≤x≤7;因为爆炸后浓度成反比例下降,所以可设y与x的函数关系式为 ![]() (k2≠0);由图象
(k2≠0);由图象![]() 过点(7,46),得到
过点(7,46),得到 ![]() ,此时自变量x的取值范围是x>7;(2)当y=34时,由y=6x+4得x=5,所以撤离的最长时间为7﹣5=2(小时),即撤离的最小速度为1.5km/h;(3)由题意知y=4
,此时自变量x的取值范围是x>7;(2)当y=34时,由y=6x+4得x=5,所以撤离的最长时间为7﹣5=2(小时),即撤离的最小速度为1.5km/h;(3)由题意知y=4![]() 时,求出x=80.5;80.5﹣7=73.5(小时);所以矿工至少在爆炸后73.5小时才能下井.
时,求出x=80.5;80.5﹣7=73.5(小时);所以矿工至少在爆炸后73.5小时才能下井.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位数,如果把它的个位数字与百位数字交换位置,那么所得的新数比原数小99,且各位数字之和为14,十位数字是个位数字与百位数字之和.求这个三位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC边AB的垂直平分线,分别交AB、BC于D、E。AE平分∠BAC. 设∠B = x(单位:度),∠C = y(单位:度).
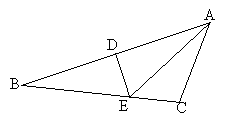
(1)求y随x变化的函数关系式,并写出自变量x的取值范围;
(2)请讨论当△ABC为等腰三角形时,∠B为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1: ![]() (即tan∠DEM=1:
(即tan∠DEM=1: ![]() ),且D,M,E,C,N,B,A在同一平面内,E,C,N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:
),且D,M,E,C,N,B,A在同一平面内,E,C,N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据: ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)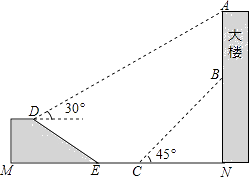
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,为满足口罩需求,某商店决定购进A,B两种口罩。若购进A口罩10盒,B口罩5盒,需要1000元。若购进A口罩4盒,B口罩3盒,需要550元.
(1)求A,B两种口罩每盒需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种口罩,考虑到市场需求,要求购进A口罩的数量不少于B口罩数量的6倍,且不超过B口罩数量的8倍,那么该商店共有几种进货方案?
(3)若销售每盒A口罩可以获利润20元,每盒B口罩可以获利润30元,在(2)的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com