
【题目】如图,![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上.
边上.
(1)如图1,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,旋转过程中,直线
,旋转过程中,直线![]() 分别与直线
分别与直线![]() 交于点
交于点![]() ,当
,当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的值;
的值;
(3)如图3,将![]() 绕点
绕点![]() 顺时针旋转,使得点
顺时针旋转,使得点![]() 在同一条直线上,点
在同一条直线上,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .猜想
.猜想![]() 和
和![]() 之间的数量关系并证明.
之间的数量关系并证明.

【答案】(1)![]() ;(2)22.5°、112.5°、45°;(3)AE+CF=
;(2)22.5°、112.5°、45°;(3)AE+CF=![]() .
.
【解析】
(1)根据勾股定理求出AB的长,可得CE,再用勾股定理可得FC的长度;
(2)分别当CM=CN,MN=CN,MN=MC时,进行讨论即可;
(3)连接AP,延长AE交CF于点Q,由四点共圆可知∠AEP=45°,从而推出A、E、Q共线,再由垂直平分线的判定可知AQ垂直平分CF,即得△ABF为等腰三角形,得到AP⊥BF,则△AEP为等腰直角三角形,得到AE和PE的关系,再根据EF和FC的关系得到AE、CF、BP三者的数量关系.
解:(1)![]() ,
,![]() ,
,![]() ,
,
∴AB=![]() =5,
=5,
∴EC=EF=3,
∴FC=![]() =
=![]() ;
;
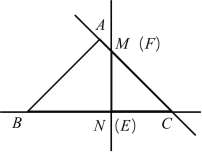
(2)由题意可知△CMN中不会形成MN=MC的等腰三角形,
①当CM=CN时,
∠CNE=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∵∠NEC=90°,
∴α=∠ACE=22.5°;
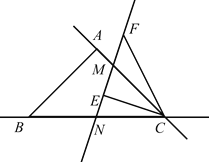
②当CM=CN时,α=∠ACE,
∵∠ACB=45°,
∴∠CNM=∠CMN=![]() ×45°=22.5°,
×45°=22.5°,
∵∠CEM=90°,
∴∠ECM=67.5°,
∴α=∠ACE=112.5°;
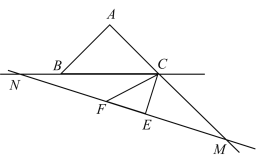
③当CN=MN时,此时CE与BC共线,
α=∠BCA=45°;
综上:当![]() 是等腰三角形时,α的值为:22.5°、112.5°、45°.
是等腰三角形时,α的值为:22.5°、112.5°、45°.
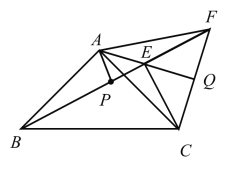
(3)AE+CF=![]()
连接AP,延长AE交CF于点Q,
由题意可得:∠CEB=∠BAC=90°,
∴A、E、C、B四点共圆,
可得:∠AEB=∠ACB=45°,
且∠CEQ=45°,
∴∠EQC=90°,
可知点A在CF的垂直平分线上,
∴AC=AF=AB,
∵点P是BF中点,
∴AP⊥BF,
∴△APE为等腰直角三角形,
∴AE=![]() ,
,
又∵△EFC为等腰直角三角形,
∴CF=![]() ,
,
∴![]() +
+![]() =
=![]() =AE+CF,
=AE+CF,
∵BP=PF,
∴AE+CF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四位自然数满足个位与百位相同,十位与千位相同,我们称这个数为“双子数”.将“双子数”![]() 的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数
的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数![]() ,记
,记![]() 为“双子数”
为“双子数”![]() 的“双11数”.例如,
的“双11数”.例如,![]() ,
,![]() ,则
,则![]() .
.
(1)计算2424的“双11数”![]() ______;
______;
(2)若“双子数”![]() 的“双11数”的
的“双11数”的![]() 是一个完全平方数,求
是一个完全平方数,求![]() 的值;
的值;
(3)已知两个“双子数”![]() 、
、![]() ,其中
,其中![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() 、
、![]() 、
、![]() 、
、![]() 都为整数,若
都为整数,若![]() 的“双11数”
的“双11数”![]() 能被17整除,且
能被17整除,且![]() 、
、![]() 的“双11数”满足
的“双11数”满足![]() ,令
,令![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市为了加强公民的节气和用气意识,按以下规定收取每月煤气费:所用煤气如果不超过50立方米,按每立方米0.8元收费;如果超过50立方米,超过部分按每立方米1.2元收费设小丽家每月所用煤气量为x立方米,应交煤气费为y元.
(1)若小丽家某月所用煤气量为80立方米,则小丽家该月应交煤气费多少元?
(2)试写出y与x之间的解析式.
(3)若小丽家4月份的煤气费为88元,则她家4月份所用煤气量为多少立方米?
(4)已知小丽家6月份所交的煤气费平均每立方米为0.95元,那么6月份小丽家用了多少立方米的煤气?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,面积为4的正方形OABC的顶点O与坐标原点重合,边OA、OC分别在x轴、y轴的正半轴上,点B、P都在函数y=![]() (x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(1)求k的值;
(2)用含m的代数式表示CD的长;
(3)求S与m之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,反比例函数y=![]() (x>0)的图象经过点A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连接AD,DC,CB.
(x>0)的图象经过点A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连接AD,DC,CB.
(1)求k的值;
(2)求证:DC∥AB;
(3)当AD∥BC时,求直线AB的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节期间某水库养殖场为适应市场需求,连续用![]() 天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第
天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第![]() 天(
天(![]() 且
且![]() 为整数)的捕捞与销售的相关信息如下:
为整数)的捕捞与销售的相关信息如下:
鲜鱼销售单价(元 |
|
单位捕捞成本(元 |
|
捕捞量 |
|
假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.
(1)求第![]() 天的收入
天的收入![]() (元)与
(元)与![]() (天)之间的函数关系式?(当天收入
(天)之间的函数关系式?(当天收入![]() 日销售额-日捕捞成本)
日销售额-日捕捞成本)
(2)在第几天![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型水果超市销售无锡水蜜桃,根据前段时间的销售经验,每天的售价x(元/箱)与销售量y(箱)有如表关系:
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)水蜜桃的进价是40元/箱,若该超市每天销售水蜜桃盈利1600元,要使顾客获得实惠,每箱售价是多少元?
(3)七月份连续阴雨,销售量减少,超市决定采取降价销售,所以从7月17号开始水蜜桃销售价格在(2)的条件下,下降了m%,同时水蜜桃的进货成本下降了10%,销售量也因此比原来每天获得1600元盈利时上涨了2m%(m<100),7月份(按31天计算)降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com