【题目】如图，
、
切
于
、
，
是弧
上任一点，过点作的切线交、于点
、
．
若
，求
的周长；
若
，
，
，你能求出的半径吗？
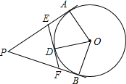
【答案】（1）8；（2）
的半径是
．
【解析】
（1）可通过切线长定理将相等的线段进行转换，得出三角形PDE的周长等于PA+PB的结论；
（2）由（1）的结论可求出PA，PB的长，利用勾股定理的逆定理可判定△PEF是直角三角形，再利用切线的性质即可证明四边形DOBF是正方形，进而求出⊙O的半径．
（1）∵EA，ED都是圆O的切线，∴EA=ED，同理FD=FB，PA=PB，∴三角形PEF的周长=PE+PF+EF=PE+EA+PF+BF=PA+PB=2PA=8，即三角形PDE的周长是8；
（2）∵PE=13，PF=12．EF=5，∴PF2+EF2=PE2=169，∴△PEF是直角三角形，∴∠EFP=90°．
∵PA=PB=
×△PEF周长，故有PA=PB=（13+12+5）=15，∴FB=PB﹣PF=15﹣12=3．
∵∠EFP=∠FDO=∠FBO=90°，OD=OB，∴四边形ODFB为正方形，∴OB=BF=3，即⊙O的半径是3．
科目：初中数学 来源： 题型：
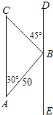
【题目】一架外国侦察机沿
方向侵入我国领空进行非法侦察，我空军的战斗机沿
方向与外国侦察机平行飞行，进行跟踪监视，我机在
处与外国侦察机
处的距离为
米，
为
，这时外国侦察机突然转向，以偏左
的方向飞行，我机继续沿方向以
米/秒的速度飞行，外国侦察机在
点故意撞击我战斗机，使我战斗机受损．问外国侦察机由到的速度是多少？（结果保留整数，参考数据
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上，若AM：MB=AN：ND=1：2，则tan∠MCN=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】织金县某中学300名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了若干名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2）．
回答下列问题：
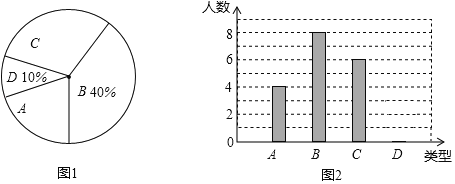
（1）在这次调查中D类型有多少名学生？
（2）写出被调查学生每人植树量的众数、中位数；
（3）求被调查学生每人植树量的平均数，并估计这300名学生共植树多少棵？
查看答案和解析>>
科目：初中数学 来源： 题型：
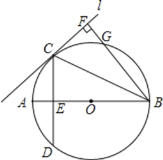
【题目】如图所示，已知AB是
的直径，直线L与相切于点C，
，CD交AB于E，
直线L，垂足为F，BF交于C．
图中哪条线段与AE相等？试证明你的结论；
若
，
，求AB的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设
，
是实数，定义关于“*”的一种运算：
．则下列结论正确的是（ ）
①若
，则
或
；
②不存在实数，，满足
；
③
；
④若
，则
．
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
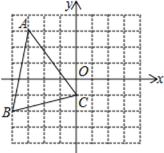
【题目】如图，在下列带有坐标系的网格中，△ABC的顶点都在边长为1的小正方形的顶点上
(1) 直接写出坐标：A__________，B__________
(2) 画出△ABC关于y轴的对称的△DEC（点D与点A对应）
(3) 用无刻度的直尺，运用全等的知识作出△ABC的高线BF（保留作图痕迹）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：
（1）在这次调查中，喜欢篮球项目的同学有 人，在扇形统计图中，“乒乓球”的百分比为 %，如果学校有800名学生，估计全校学生中有 人喜欢篮球项目．
（2）请将条形统计图补充完整．
（3）在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
