
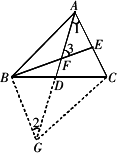
如图所示,已知AD为△ABC的中线,点E为AC上的一点,连接BE交AD于点F,且AE=FE,求证:AC=BF.
|
分析:要证AC和BF相等,从学过的方法可联想等边对等角或平行四边形的判定和性质,从图中可以看出:边、角关系比较分散,联系不到一起,这就需要构造图形把已知条件联系起来.由题可知,点D为BC的中点,也可看作平行四边形一条对角线的中点,故只要把另一条对角线作出来,就构成了平行四边形,由此该问题得以解决 证明:延长AD到点G,使DG=AD,连接BG,CG. 因为DG=AD,BD=CD, 所以四边形ABGC是平行四边形. 所以AC∥BG,AC=BG.所以∠1=∠2. 又因为AE=FE,所以∠1=∠3. 所以∠2=∠3=∠BFG.所以BG=BF. 又因为BG=AC,所以BF=AC. 点评:当题中有三角形的中线时,常利用中线构造平行四边形,然后利用平行四边形的性质解答. |


科目:初中数学 来源: 题型:
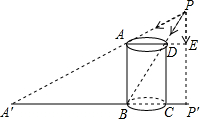 一圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP′=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为A′,求点A′到CD的距离.
一圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP′=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为A′,求点A′到CD的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
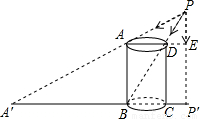
 一圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP′=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为A′,求点A′到CD的距离.
一圆柱形器皿在点光源P下的投影如图所示,已知AD为该器皿底面圆的直径,且AD=3,CD为该器皿的高,CD=4,CP′=1,点D在点P下的投影刚好位于器皿底与器皿壁的交界处,即点B处,点A在点P下的投影为A′,求点A′到CD的距离.查看答案和解析>>
科目:初中数学 来源:2011年安徽省中考说明数学检测卷(四)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com