练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．计算$\frac{1}{4}$-$\frac{2}{3}$的结果是-$\frac{5}{12}$．

    分析 根据有理数的减法运算法则进行计算即可得解．

    解答 解：$\frac{1}{4}$-$\frac{2}{3}$，
    =$\frac{3}{12}$-$\frac{8}{12}$，
    =-$\frac{5}{12}$．
    故答案为：-$\frac{5}{12}$．

    点评 本题考查了有理数的减法，熟记运算法则是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．下列对函数的认识正确的是（　　）
    A．若y是x的函数，那么x也是y的函数
    B．两个变量之间的函数关系一定能用数学式子表达
    C．若y是x的函数，则当y取一个值时，一定有唯一的x值与它对应
    D．一个人的身高也可以看作他年龄的函数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

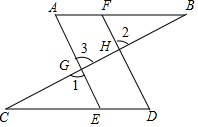    2．请把以下证明过程补充完整，并在下面的括号内填上推理理由：
    已知：如图，∠1=∠2，∠A=∠D．
    求证：∠B=∠C
    证明：∵∠1=∠2，（已知）
    又：∵∠1=∠3，对顶角相等
    ∴∠2=∠3，（等量代换）
    ∴AE∥FD同位角相等，两直线平行
    ∴∠A=∠BFD两直线平行，同位角相等
    ∵∠A=∠D（已知）
    ∴∠D=∠BFD（等量代换）
    ∴AB∥CD内错角相等，两直线平行
    ∴∠B=∠C两直线平行，内错角相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．在△ABC中，∠C=90°，下列选项中的关系式正确的是（　　）
    A．sinA=$\frac{AC}{AB}$B．cosB=$\frac{AC}{BC}$C．tanA=$\frac{BC}{AB}$D．AC=AB•cosA

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

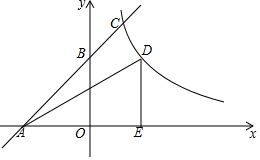    6．在平面直角坐标系内，点O为坐标原点，直线y=x+4交x轴于点A，交y轴于点B，点C（2，m）在直线y=x+4上，反比例函数
    y=$\frac{n}{x}$经过点C．
    （1）求m，n的值；
    （2）点D在反比例函数y=$\frac{n}{x}$的图象上，过点D作X轴的垂线，点E为垂足，若OE=3，连接AD，求tan∠DAE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

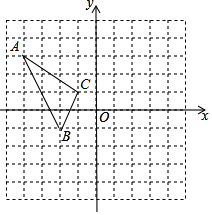    16．如图，在平面直角坐标系中，△ABC的顶点A（-4，3），B（-2，-1），C（-1，1）均在正方形网格的格点上，画出△ABC关于y轴对称的△A1B1C1，并写出点A的对应点A1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知：y=$\sqrt{x-2017}$-$\sqrt{2017-x}$-2016，求x+y的平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（　　）
    A．∠M=∠NB．AB=CDC．AM=CND．AM∥CN

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

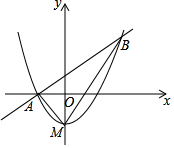    1．如图，顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点，且点A在x轴上，点B的横坐标为2，连结AM、BM．
    （1）求抛物线的函数关系式；
    （2）判断△ABM的形状，并说明理由．

    查看答案和解析>>

    同步练习册答案