
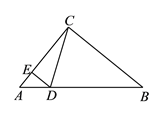
【题目】如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E.设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P,问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.
【答案】是,理由见解析.
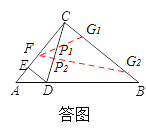
【解析】试题分析:分三种情况讨论:①若∠CFG1=∠ECD,此时线段CP是△CFG1的FG1边上的中线;②若∠CFG2=∠EDC,此时线段CP为△CFG2的FG2边上的高线;③当CD为∠ACB的平分线时,CP既是△CFG的FG边上的高线又是中线.
试题解析:
①若![]() ,此时线段CP1为△CFG1的斜边FG1上的中线.证明如下:
,此时线段CP1为△CFG1的斜边FG1上的中线.证明如下:
∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() . ∴
. ∴![]() .
.
又∵![]() ,∴
,∴![]() . ∴
. ∴![]() .
.
∴线段CP1为△CFG1的斜边FG1上的中线.
②若![]() ,此时线段CP2为△CFG2的斜边FG2上的高线.证明如下:
,此时线段CP2为△CFG2的斜边FG2上的高线.证明如下:
∵![]() ,
,
又∵DE⊥AC,∴![]() . ∴
. ∴![]() .
.
∴![]() . ∴CP2⊥FG2.
. ∴CP2⊥FG2.
∴线段CP2为△CFG2的斜边FG2上的高线.
③当CD为∠ACB的平分线时,CP既是△CFG的FG边上的高线又是中线.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
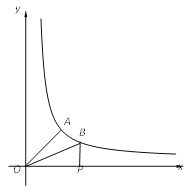
【题目】如图,已知A、B是反比例函数y=![]() 图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP=
图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP=![]() .
.
(1)求点A的坐标;
(2)连接AB,求四边形AOPB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( ) 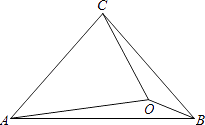
A.55°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
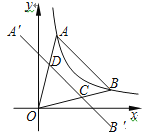
【题目】如图,点A,B在反比例函数y=![]() (x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为
(x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为![]() ,则点A的坐标为_______.
,则点A的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
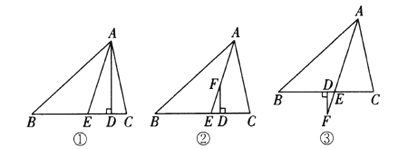
【题目】在![]() 中,
中,![]() .如图①,
.如图①,![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,则易知
,则易知![]() .
.
(1)如图②,![]() 平分
平分![]() ,
, ![]() 为
为![]() 上的一点,且
上的一点,且![]() 于点
于点![]() ,这时
,这时![]() 与
与![]() 、
、![]() 有何数量关系?请说明理由;
有何数量关系?请说明理由;
(2)如图③,![]() 平分
平分![]() ,
,![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 于点
于点![]() ,请你写出这时
,请你写出这时![]() 与
与![]() 、
、![]() 之间的数量关系(只写结论,不必说明理由).
之间的数量关系(只写结论,不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=![]() 的图象经过D点.
的图象经过D点.

(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com