
【题目】综合与探究
如图1,在平面直角坐标系中,点![]() 是坐标原点,点
是坐标原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 是菱形,直线
是菱形,直线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

(1)点![]() 的坐标是______;
的坐标是______;
(2)求直线![]() 的函数解析式;
的函数解析式;
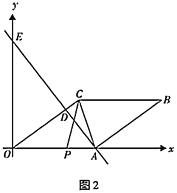
(3)如图2,动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以1个单位长度/秒的速度向终点
方向以1个单位长度/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式(要求写出自变量
之间的函数关系式(要求写出自变量![]() 的取值范围)
的取值范围)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() 或
或![]()
![]() .
.
【解析】
(1)由点C坐标求OC的长,得到菱形边长为5,再根据CB∥x轴且CB=OC=5,即求出点B坐标;
(2)过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,由点C的坐标求出OF,CF的长,然后证得
轴,由点C的坐标求出OF,CF的长,然后证得![]() ,得出OD,AD的长,根据三角形的面积求出DH,再根据勾股定理求得OH,即可得点D坐标,然后利用待定系数法求得AD的解析式;
,得出OD,AD的长,根据三角形的面积求出DH,再根据勾股定理求得OH,即可得点D坐标,然后利用待定系数法求得AD的解析式;
(3)由点P在折线OAB上运动可知需分两种情况讨论.当点![]() 在
在![]() 边上运动时,根据
边上运动时,根据![]() 即可得出S与t的关系式;当点
即可得出S与t的关系式;当点![]() 在
在![]() 边上运动时,过点
边上运动时,过点![]() 作
作![]() ,可得
,可得![]() .根据
.根据![]() 即可得出S与t的关系式.
即可得出S与t的关系式.
解:(1)过点C作CF⊥x轴于点F,

∴∠CFO=90°
∵点C的坐标为(4,3),
∴OF=4,CF=3
∴OC=![]() =
=![]() =5,
=5,
∵四边形OABC是菱形,
∴OA=BC=OC=5,BC∥x轴,
∴yB=yC=3,xB=xC+5=9,
故答案为:(9,3);
(2)如答图1,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,

∵点![]() 的坐标为
的坐标为![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() .
.
∵四边形![]() 为菱形,
为菱形,
∴![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,

∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴ .
.
∴![]() .
.
设直线![]() 的函数解析式为
的函数解析式为![]() .
.
∵
解得
∴直线![]() 的函数解析式为
的函数解析式为![]() .
.
(3)分两种情况:
①当点![]() 在
在![]() 边上运动时,
边上运动时,
∴![]()
![]() .
.
②如答图2,当点![]() 在
在![]() 边上运动时,
边上运动时,
由(2)得![]() ,
,
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∴![]() .
.
∴![]()
![]() .
.



 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=x+b与x轴交于点A(2,0),P为y轴上B点下方一点,以AP为腰作等腰直角三角形APM,点M落在第四象限,若PB=m(m>0),用含m的代数式表示点M的坐标是( )

A.(m-2,m+4)B.(m+2,m+4)C.(m+2,-m-4)D.(m-2,-m-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
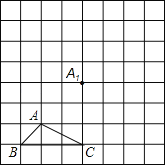
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,得到△A1B2C2,在网格中画出旋转后的△A1B2C2.
(3)连结![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.

(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某排球队6名上场队员的身高(单位:![]() )是:180,184,188,190,192,194,现用一名身高为
)是:180,184,188,190,192,194,现用一名身高为![]() 的队员换下场上身高为
的队员换下场上身高为![]() 的队员,与换人前相比,场上队员的身高平均数________.填“变大”.“不变”.“变小”),方差________.(填“变大”.“不变”.“变小”)
的队员,与换人前相比,场上队员的身高平均数________.填“变大”.“不变”.“变小”),方差________.(填“变大”.“不变”.“变小”)
查看答案和解析>>
科目:初中数学 来源: 题型:
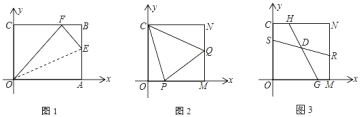
【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4![]() ,求RS的长.
,求RS的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
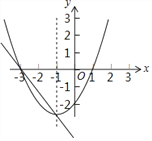
【题目】已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:
①二次函数y1有最大值;
②二次函数y1的图象关于直线x=﹣1对称
③当x=﹣2时,二次函数y1的值大于0
④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<﹣3或m>﹣1.
以上推断正确的是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com