
【题目】定义:在平面直角坐标系中,O为坐标原点,对于任意两点P(m,y)Q(m,y0),m为任意实数.若y0=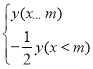 ,则称点Q是点P的变换点.例如:若点P(1,y)在直线y=x上,点P的变换点Q在函数y=
,则称点Q是点P的变换点.例如:若点P(1,y)在直线y=x上,点P的变换点Q在函数y=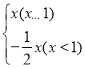 的图象上设点P(m,y)在函数y=﹣x2+2x+3的图象上,点P的变换点Q所在的图象记为G.
的图象上设点P(m,y)在函数y=﹣x2+2x+3的图象上,点P的变换点Q所在的图象记为G.
(1)求图象G对应的函数关系式;
(2)设图象G与x轴的交点为A、B(点A在点B的左侧)与y轴交于点C,连结AC、BC,求△ABC的面积;
(3)当﹣2≤x≤m时,若图象G的最高点与最低点之间的距离不大于![]() ,直接写出m的取值范围;
,直接写出m的取值范围;
(4)设点P(![]() ,y)在函数y=ax2﹣3ax﹣4a(a≠0)的图象上,点P的变换点Q所在的图象记为G1,图象G1与x轴的交点为M、N(点M在点N的左侧),连结MN,将MN沿y轴向上平移一个单位得到线段M'N',当图象G1与线段M'N'只有一个交点时,求a的取值范围.
,y)在函数y=ax2﹣3ax﹣4a(a≠0)的图象上,点P的变换点Q所在的图象记为G1,图象G1与x轴的交点为M、N(点M在点N的左侧),连结MN,将MN沿y轴向上平移一个单位得到线段M'N',当图象G1与线段M'N'只有一个交点时,求a的取值范围.
【答案】(1)y=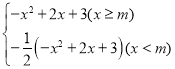 ,(2)6或3;(3)1﹣
,(2)6或3;(3)1﹣![]() ≤m≤0或1≤m≤1+
≤m≤0或1≤m≤1+![]() 或3≤m≤1+
或3≤m≤1+![]() 或m≥4;(4)a
或m≥4;(4)a![]() 或0<a<
或0<a<![]() .
.
【解析】
(1)由题意得:函数G的表达式为:y=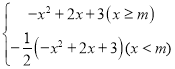 ,
,
(2)点A、B的坐标分别为(﹣1,0)、(3,0),点C(0,3)或(0,﹣![]() ),故△ABC的面积=
),故△ABC的面积=![]() ×AB×OC=6或3;
×AB×OC=6或3;
(3)分m≤﹣1、﹣1≤m≤1、1≤m≤3、m≥3三种情况,分别求解即可;
(4)分当a<0、a>0两种情况求解即可.
解:(1)由题意得:
函数G的表达式为:y=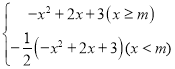 ,
,
(2)如图1,令y=0,
解得:x=﹣1或3,
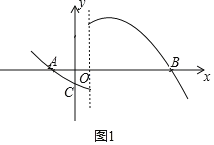
故点A、B的坐标分别为:(﹣1,0)、(3,0),
函数对称轴为:x=1,
点C(0,3)或(0,﹣![]() );
);
故△ABC的面积=![]() ×AB×OC=6或3;
×AB×OC=6或3;
(3)①当m≤﹣1时,如图2,
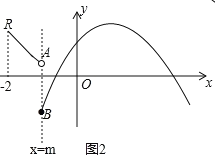
当﹣2≤x≤m时,图象G的最高点为R,最低点B,点R(﹣2,![]() ),
),
则yR﹣yB![]() ,
,
即![]() ﹣(﹣m2+2m+3)
﹣(﹣m2+2m+3)![]() ,
,
解得:1﹣![]() ≤m≤1+
≤m≤1+![]() ,
,
故1﹣![]() ≤m≤﹣1;
≤m≤﹣1;
②当﹣1≤m≤1时,如图3所示,点A(﹣2,![]() )
)
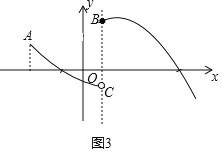
当点A为最高点时,
yA﹣yC![]() ,
,
即![]() +
+![]() (﹣m2+2m+3)
(﹣m2+2m+3)![]() ,
,
解得:m为任意实数;
点B是高点时,
yB﹣yC![]() ,
,
即![]() (﹣m2+2m+3)
(﹣m2+2m+3)![]() ,
,
解得:m≥2或m≤0,
故﹣1≤m≤0;
③当1≤m≤3时,如图4所示,点A(﹣2,![]() ),顶点E(1,﹣2),
),顶点E(1,﹣2),
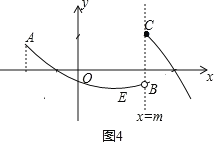
当点A是最高点时,
yA﹣yE=![]() ,符合条件;
,符合条件;
当点C是最高点时,
yC﹣yE![]() ,
,
即![]() (﹣m2+2m+3)
(﹣m2+2m+3)![]() ,
,
解得:1﹣![]() ≤m≤1
≤m≤1![]() ,
,
故1≤m≤1+![]() ;
;
④当m≥3时,如图5所示,点A(﹣2,![]() ),顶点E(1,﹣2),
),顶点E(1,﹣2),
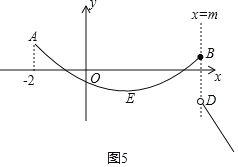
(Ⅰ)当点A是最高点时,
当点E是最低点时,yA﹣yE=![]() ;
;
当点D时最低点时,yA﹣yD![]() ,
,
即![]() ﹣(﹣m2+2m+3)
﹣(﹣m2+2m+3)![]() ,
,
解得:3≤m≤1+![]() ;
;
故3≤m≤1+![]() ;
;
(Ⅱ)当点B是最高点时,
当点E是最低点时,yB﹣yE=![]() ,同理可得:m≥4,
,同理可得:m≥4,
当点D时最低点时,yB﹣yD≤![]() ,同理可得:m≤1+
,同理可得:m≤1+![]() ,
,
故:3≤m≤1+![]() 或m≥4;
或m≥4;
综上,1﹣![]() ≤m≤0或1≤m≤1+
≤m≤0或1≤m≤1+![]() 或3≤m≤1+
或3≤m≤1+![]() 或m≥4;
或m≥4;
(4)①当a<0时,如图6所示,
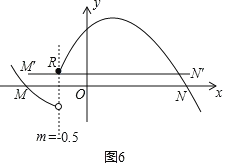
当x=﹣![]() 时,对应抛物线上的实点R,则yR>1,
时,对应抛物线上的实点R,则yR>1,
即:y=ax2﹣3ax﹣4a=a(![]() +
+![]() ﹣4)>1,
﹣4)>1,
解得:a![]() ,
,
②当a>0时,
当x=﹣![]() 时,﹣
时,﹣![]() (ax2﹣3ax﹣4a)<1,
(ax2﹣3ax﹣4a)<1,
即﹣![]() a(
a(![]() +
+![]() ﹣4)<1,
﹣4)<1,
解得:a![]() ,即0<a<
,即0<a<![]() ;
;
综上,a的取值范围为:a![]() 或0<a<
或0<a<![]() .
.


科目:初中数学 来源: 题型:
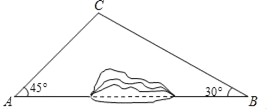
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
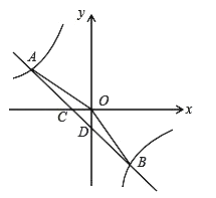
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的
的图象交于第二、四象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,连接
,连接![]() ,且
,且![]() .
.
(1)求这个反比例函数和一次函数的解析式;
(2)根据图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
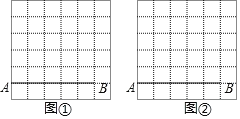
【题目】图①、图②都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB的端点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
(1)在图①中画出一个以AB为一边的等腰△ABC,使点C在格点上,且面积为![]() ;
;
(2)在图②中画出一个以AB为一边的等腰△ABD,使点D在格点上,且tan∠DAB=3,并直接写出△ABD底边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
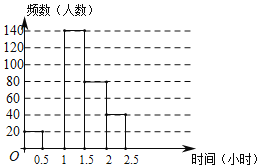
【题目】某区规定学生每天户外体育活动时间不少于1小时,为了解学生参加户外体育活动的情况,对部分学生每天参加户外体育活动的时间进行了随机抽样调查,并将调查结果绘制成如图的统计图表(不完整).请根据图表中的信息,解答下列问题:
(1)表中的a=_____,将频数分布直方图补全;
(2)该区8000名学生中,每天户外体育活动的时间不足1小时的学生大约有多少名?
(3)若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名,请用画树状图或列表法求恰好抽到1名男生和1名女生的概率.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t<0.5 | 20 | 0.05 |
B | 0.5≤t<1 | a | 0.3 |
C | l≤t<1.5 | 140 | 0.35 |
D | 1.5≤t<2 | 80 | 0.2 |
E | 2≤t<2.5 | 40 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用画树状图的方法画出的某个试验的所有可能发生的结果,则这个试验不可能是( )
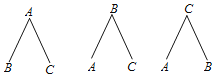
A.在一个不透明的袋中有3个除颜色外完全相同的小球,其中两个黑球,一个白球,从中随机取出两个球
B.小明,小王两个人在一个路口,分别从直行,左转,右转三个方向中随机选一个方向
C.从某学习小组的两名男生和一名女生中随机选取两名学生进行竞答
D.体育测试中,随机从足球运球,篮球运球,排球垫球三个项目中选择两个项目
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据天气预报报道,福建省部分城市某日的最高气温如下表所示:
城市 | 福州 | 厦门 | 宁德 | 莆田 | 泉州 | 漳州 | 龙岩 | 三明 | 南平 |
最高气温(℃) | 11 | 16 | 11 | 13 | 13 | 17 | 16 | 11 | 9 |
则下列说法正确的是( )
A.龙岩的该日最高气温最高B.这组数据的众数是16
C.这组数据的中位数是11D.这组数据的平均数是13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com