
 的图象相交于B(-1,5)、C(
的图象相交于B(-1,5)、C(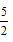 ,d)两点,点P (m ,n )是一次函数y1=kx+b的图象上的动点。
,d)两点,点P (m ,n )是一次函数y1=kx+b的图象上的动点。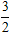 ,过点P作x轴的平行线与函数y2=
,过点P作x轴的平行线与函数y2=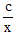 的图象相交于点D,试问△PAD的面积是否存在最大值?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由;
的图象相交于点D,试问△PAD的面积是否存在最大值?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由; 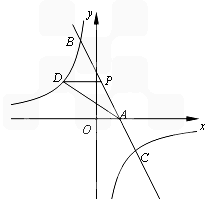
解:(1)将点B 的坐标代入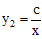 ,得
,得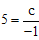 ,解得c=-5。
,解得c=-5。
∴反比例函数解析式为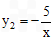 ,
,
将点C(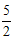 ,d)的坐标代入
,d)的坐标代入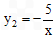 ,得
,得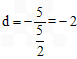 ,
,
∴C(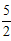 ,-2),
,-2),
∵一次函数y1=kx+b的图象经过B(-1,5)、C(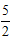 ,-2)两点,
,-2)两点,
∴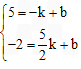 ,
,
解得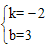 ;
;
(2)存在,
令y1=0,即-2x+3=0,解得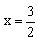 ,
,
∴A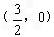 ,
,
由题意,点P(m,n)是一次函数y1=-2x+3的图像上的动点,且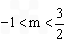 ,
,
∴点P在线段AB上运动(不含A、B)
设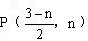
∴DP∥x轴,且点D在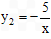 的图象上,
的图象上,
∴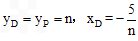 ,即D(
,即D(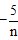 ,n)。
,n)。
∴△PAD的面积为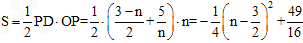 。
。
∴S关于n的二次函数的图象开口向下,有最大值,
又∵n=-2m+3,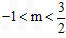 ,得0<n<5,而
,得0<n<5,而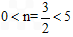 ,
,
∴当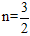 时,即
时,即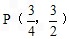 时,△PAD的面积S最大,为
时,△PAD的面积S最大,为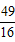 ;
;
(3)由已知,P(
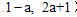 ),
),
易知m≠n,即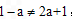 ,即a≠0,
,即a≠0,
若a>0,则m<1<n,
由题设,m>0,n≤2,解出不等式组的解为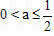 ,
,
若a<0,则n<1<m,
由题设,n≥0,m<2,解出不等式组的解为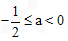 ,
,
综上所述,数a的取值范围为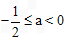 ,
,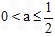 。
。


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
| a | x |
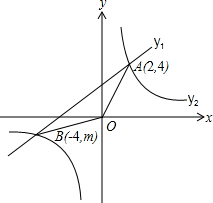 B(-4,m)两点.
B(-4,m)两点.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=-| 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数y2=
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数y2=| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数y=
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数y=| k2 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=kx+b的图象交反比例函数y=
如图,已知一次函数y=kx+b的图象交反比例函数y=| 4-2m |
| x |
| BC |
| AB |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com