
【题目】如图,在美化校园的活动中,数学兴趣小组用16m长的篱笆,一边靠墙围成一个矩形花园ABCD,墙长为6m,设AB![]() m.
m.
(1)若花园的面积为14![]() ,求
,求![]() 的值;
的值;
(2)花园的面积能否为40![]() ?为什么?
?为什么?
(3)若要求花园的面积大于24![]() ,求
,求![]() 的取值范围.
的取值范围.

【答案】(1)2;(2)花园的面积不能为40![]() ,理由详见解析;(3)4<
,理由详见解析;(3)4<![]() ≤6.
≤6.
【解析】
(1)根据矩形的面积公式列出方程求解即可;
(2)根据矩形的面积计算公式列出连长与面积的二次函数关系式,计算出最大值,与40![]() 比较即可;
比较即可;
(3)先确定矩形面积等于24时,x的取值,再确定花园的面积大于24![]() 时
时![]() 的取值范围.
的取值范围.
(1)由题意列方程:![]() ,
,
解得![]() 14,
14,![]() 2,
2,
由于![]() 14>6不合题意,所以
14>6不合题意,所以![]() =2.
=2.
(2)设花园的面积为![]()
![]() ,依题意有:
,依题意有:
![]() ,即
,即![]() ,
,
![]() 的最大值=32,
的最大值=32,
∴花园的面积不能为40![]() .
.
(3)由(2)知![]() ,
,
当![]() =24时,有
=24时,有![]() ,解得
,解得![]() 12,
12,![]() 4,
4,
∵花园的面积大于24![]() ,∴4<
,∴4<![]() <12,
<12,
又∵墙长为6m,∴0<![]() ≤6,
≤6,
∴![]() 的取值范围是4<
的取值范围是4<![]() ≤6.
≤6.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图1,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 为常数)经过点A
为常数)经过点A![]() 和B
和B![]() .
.
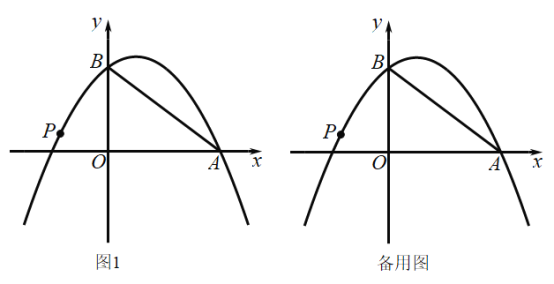
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 是该抛物线上的一动点,设点
是该抛物线上的一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①当![]() 是以
是以![]() 为直角边的直角三角形时,求
为直角边的直角三角形时,求![]() 的值;
的值;
②若![]() 满足
满足![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
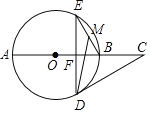
【题目】如图,点C是⊙O的直径AB延长线上一点,过⊙O上一点D作DF⊥AB于F,交⊙O于点E,点M是BE的中点,AB=4,∠E=∠C=30°.
(1)求证:CD是⊙O的切线;
(2)求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
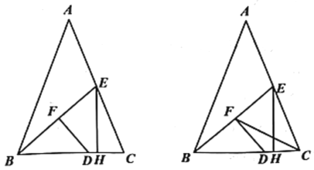
【题目】已知:如图1,△ABC中,AB=AC,BC=6,BE为中线,点D为BC边上一点;BD=2CD,DF⊥BE于点F,EH⊥BC于点H.
(1)CH的长为_____;
(2)求BF·BE的值:
(3)如图2,连接FC,求证:∠EFC=∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() )的图象如图所示,对称轴为
)的图象如图所示,对称轴为![]() .有下列4个结论:①
.有下列4个结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 的增大而增大.其中,正确的结论有( )
的增大而增大.其中,正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并解决问题:
《名画》中的数学
前苏联著名科学家别莱利曼在他所著的《趣味代数学》中介绍了波格达诺夫·别列斯基的《名画》,画上那位老师拉金斯基是一位自然科学教授,放弃了大学教席(教师职务)来到农村学校当一名普通老师.画中,黑板上写着一道式子,如图所示:

从这道算式计算可以得出答案等于2,如果仔细一研究,10,11,12,13,14这几个数具有一种有趣的特性:![]() ,而且
,而且![]() .
.
请解答以下问题:
(1)还有没有其他像这样五个连续的整数,前三个数的平方和正好等于后两个数的平方和呢?如果有,请求出另外的五个连续的整数;
(2)若七个连续整数前四个数的平方和等于后三个数的平方和,请直接写出符合条件的连续整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
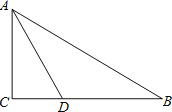
【题目】已知:如图,在![]() 中,
中,![]() 的角平分线
的角平分线![]() 交
交![]() 边于
边于![]() .
.
(1)以![]() 边上一点
边上一点![]() 为圆心,过
为圆心,过![]() 两点作
两点作![]() (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若(1)中的![]() 与
与![]() 边的另一个交点为
边的另一个交点为![]() ,
,![]() ,求线段
,求线段![]() 与劣弧
与劣弧![]() 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com