
【题目】如图①,在平面直角坐标系中,直线![]() :
:![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() :
:![]() 交于点
交于点![]() ,以线段
,以线段![]() 为边在直线
为边在直线![]() 的下方作正方形
的下方作正方形![]() ,此时点
,此时点![]() 恰好落在
恰好落在![]() 轴上.
轴上.
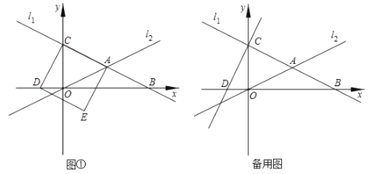
(1)求出![]() 三点的坐标.
三点的坐标.
(2)求直线![]() 的函数表达式.
的函数表达式.
(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的一个动点,在平面内是否存在点
上的一个动点,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]()
![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,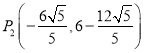 ,
,![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点B,C的坐标,联立直线l1,l2的解析式成方程组,通过解方程组可求出点A的坐标;
(2)过点A作AF⊥y轴,垂足为点F,则△ACF≌△CDO,利用全等三角形的性质可求出点D的坐标,根据点C,D的坐标,利用待定系数法即可求出直线CD的解析式;
(3)分OC为对角线及OC为边两种情况考虑:①若OC为对角线,由菱形的性质可求出点P的纵坐标,再利用一次函数图象上点的坐标特征可求出点P1的坐标;②若OC为边,设点P的坐标为(m,2m+6),分CP=CO和OP=OC两种情况,利用两点间的距离公式可得出关于m的方程,解之取其负值,再将其代入点P的坐标中即可得出点P2,P3的坐标.
(1)∵直线![]() :
:![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() ,
,
解方程组: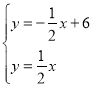 得:
得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)如图1,作![]() ,则
,则![]() ,
,
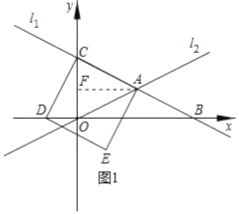
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 、
、![]() 代入得:
代入得:![]() ,
,
解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]()
(3)存在
①以![]() 为对角线时,如图2所示,
为对角线时,如图2所示,
则PQ垂直平分CO,
则点P的纵坐标为:![]() ,
,
当y=3时,![]() ,解得:x=
,解得:x=![]()
∴点![]() ;
;
②以![]() 为边时,如图2,设点P(m,2m+6),
为边时,如图2,设点P(m,2m+6),
当CP=CO时,![]() ,
,
解得:![]() (舍去)
(舍去)
∴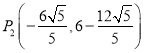 ,
,
当OP=OC时,![]() ,
,
解得:![]() (舍去)
(舍去)
∴![]()
综上所述,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,
为顶点的四边形是菱形,![]() ,
,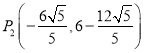 ,
,![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师出了这样一道题:甲、乙两地相距1400km,乘高铁列车从甲地到乙地比乘特快列车少用9h,已知高铁列车的平均行驶速度是特快列车的2.8倍.求高铁列车从甲地到乙地的时间.
老师要求同学先用列表方式分析再解答.下面是两个小组分析时所列的表格:
小组甲:设特快列车的平均速度为![]() km/h.
km/h.
时间/h | 平均速度/(km/h) | 路程/km | |
高铁列车 | 1400 | ||
特快列车 |
| 1400 |
小组乙:高铁列车从甲地到乙地的时间为![]() h.
h.
时间/h | 平均速度/(km/h) | 路程/km | |
高铁列车 |
| 1400 | |
特快列车 | 1400 |
(1)根据题意,填写表格中空缺的量;
(2)结合表格,选择一种方法进行解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 y=﹣![]() x+4 与坐标轴分别交于 A,B 两点,把△AOB 绕点A 逆时针旋转 90°后得到△AO′B′.
x+4 与坐标轴分别交于 A,B 两点,把△AOB 绕点A 逆时针旋转 90°后得到△AO′B′.
(1)写出点 A 的坐标,点 B 的坐标;
(2)在方格中直接画出△AO′B′;
(3)写出点 O′的坐标;点 B′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年某园林绿化公司购回一批香樟树,全部售出后利润率为20%.
(1)求 2016年每棵香樟树的售价与成本的比值.
(2)2017年,该公司购入香樟树数量增加的百分数与每棵香樟树成本降低的百分数均为a,经测算,若每棵香樟树售价不变,则总成本将比2016年的总成本减少8万元;若每棵香樟树售价提高百分数也为a,则销售这批香樟树的利润率将达到4a.求a的值及相应的2017年购买香樟树的总成本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]()
![]() 交于A点,且点A的横坐标是4.双曲线
交于A点,且点A的横坐标是4.双曲线![]()
![]() 上有一动点C(m,n),
上有一动点C(m,n), ![]() .过点A作
.过点A作![]() 轴垂线,垂足为B,过点C作
轴垂线,垂足为B,过点C作![]() 轴垂线,垂足为D,联结OC.
轴垂线,垂足为D,联结OC.

(1)求![]() 的值;
的值;
(2)设![]() 的重合部分的面积为S,求S与m的函数关系;
的重合部分的面积为S,求S与m的函数关系;
(3)联结AC,当第(2)问中S的值为1时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
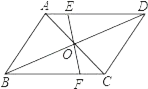
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com