
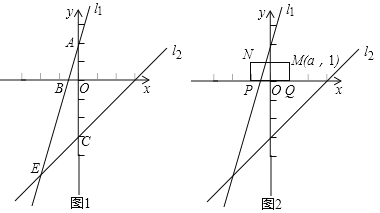
【题目】如图1,在直角坐标系中,一次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图象
的图象![]() 交于点
交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与y轴交于点
与y轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)如图2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的边
的边![]() 在
在![]() 轴上平移,若矩形
轴上平移,若矩形![]() 与直线
与直线![]() 或
或![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围,
的取值范围,
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由点![]() 在一次函数
在一次函数![]() 图象上可求出E点坐标,然后将AE两点坐标代入解析式即可求出l1的表达式;
图象上可求出E点坐标,然后将AE两点坐标代入解析式即可求出l1的表达式;
(2)由于![]() ,求出BC坐标即可解答
,求出BC坐标即可解答
(3)分别求出矩形MNPQ与直线l1或l2有交点边界时的极限值可解答
(1)∵点![]() 在一次函数
在一次函数![]() 图象上,
图象上,
∴![]() ,
,
∴![]() ;
;
设直线![]() 的表达式为
的表达式为![]() ,
,
∵直线![]() 过点
过点![]() 和
和![]() ,
,
∴![]() ,
,
解得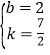 .
.
∴直线![]() 的表达式为
的表达式为![]() .
.
(2)由(1)可知:![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
∴![]()
![]() .
.
(3)![]() 或
或![]() .
.
当Q在直线![]() 上时,a=
上时,a=![]() ,此时矩形MNPQ与直线
,此时矩形MNPQ与直线![]() 有交点a取最小值,
有交点a取最小值,
当N在直线![]() 上时,N点坐标=
上时,N点坐标=![]() ,a=
,a=![]() ,此时矩形MNPQ与直线
,此时矩形MNPQ与直线![]() 有交点a取最大值,
有交点a取最大值,
当Q在直线![]() 上时,a=2,此时矩形MNPQ与直线
上时,a=2,此时矩形MNPQ与直线![]() 有交点a取最小值,
有交点a取最小值,
当N在直线![]() 上时,N点坐标=4,a=6,此时矩形MNPQ与直线
上时,N点坐标=4,a=6,此时矩形MNPQ与直线![]() 有交点a取最大值,
有交点a取最大值,
故当![]() 时,矩形MNPQ与直线
时,矩形MNPQ与直线![]() 有交点,当2≤a≤6时,矩形MNPQ与直线
有交点,当2≤a≤6时,矩形MNPQ与直线![]() 有交点,
有交点,


科目:初中数学 来源: 题型:
【题目】某大学公益组织计划购买![]() 两种的文具套装进行捐赠,关注留守儿童经洽谈,购买
两种的文具套装进行捐赠,关注留守儿童经洽谈,购买![]() 套装比购买
套装比购买![]() 套装多用20元,且购买5套
套装多用20元,且购买5套![]() 套装和4套
套装和4套![]() 套装共需820元.
套装共需820元.
(1)求购买一套![]() 套装文具、一套
套装文具、一套![]() 套装各需要多少元?
套装各需要多少元?
(2)根据该公益组织的募捐情况和捐助对象情况,需购买![]() 两种套装共60套,要求购买
两种套装共60套,要求购买![]() 两种套装的总费用不超过5240元,则购买
两种套装的总费用不超过5240元,则购买![]() 套装最多多少套?
套装最多多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
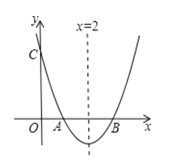
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)根据图像,直接写出不等式x2+bx+c>0的解集: .
(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为(3,5),(6,1).若过原点的直线l将这个图案分成面积相等的两部分,则直线l的函数解析式为_____.
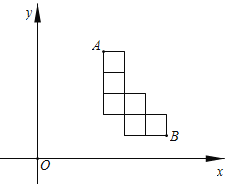
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解七年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5﹣46.5;B:46.5﹣53.5;C:53.5﹣60.5;D:60.5﹣67.5;E:67.5﹣74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

请解答下列问题:
(1)这次随机抽取了 名学生调查,并补全频数分布直方图;
(2)在抽取调查的若干名学生中体重在 组的人数最多,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校七年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解决问题:
材料1:对于一个三位数其十位数字等于个位数字与百位数字的差的两倍,则我们称这样的数为“倍差数”如122,![]() ;
;
材料2:若一个数![]() 能够写成
能够写成![]() 均为正整数,且
均为正整数,且![]() ,则我们称这样的数为“不完全平方差数”,
,则我们称这样的数为“不完全平方差数”,![]() 最大时,我们称此时的
最大时,我们称此时的![]() 、
、![]() 为
为![]() 的一组“最优分解数”,井规定
的一组“最优分解数”,井规定![]() .例如
.例如![]() ,因为:
,因为:![]() ,
,![]() ,
,![]() ,所以
,所以![]() ;
;
(1)求证:任意的一个“倍差数”与其百位数字之和能够被3整除;
(2)若一个小于300的三位数![]() 其中
其中![]() ,
,![]() ,且
,且![]() 均为整数)既是一个“不完全平方差数”,也是一个“倍差数”,求所有
均为整数)既是一个“不完全平方差数”,也是一个“倍差数”,求所有![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com