
【题目】在平面直角坐标系xOy中,直线y=x+1与x轴、y轴分别交于点A,B,抛物线y=ax2+bx-3a(a>0)经过点A将点B向右平移5个单位长度,得到点C.
(1)求点C的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
【答案】(1)C(5,1);(2)抛物线的对称轴x=1;(3)a≥![]() 或a<-
或a<-![]() 或a=-
或a=-![]() .
.
【解析】
(1)根据坐标轴上点的坐标特征可求点B的坐标,根据平移的性质可求点C的坐标;
(2)根据坐标轴上点的坐标特征可求点A的坐标,进一步求得抛物线的对称轴;
(3)结合图形,分三种情况:①a>0;②a<0,③抛物线的顶点在线段BC上;进行讨论即可求解.
(1)与y轴交点:令x=0代入直线y=x+1得y=1,
∴B(0,1),
∵点B向右平移5个单位长度,得到点C,
∴C(5,1);
(2)与x轴交点:令y=0代入直线y=x+1得x=-1,
∴A(-1,0),
∵将点A(-1,0)代入抛物线y=ax2+bx-3a中得0=a-b-3a,即b=-2a,
∴抛物线的对称轴x=-![]() ;
;
(3)∵抛物线y=ax2+bx-3a经过点A(-1,0)且对称轴x=1,
由抛物线的对称性可知抛物线也一定过A的对称点(3,0),
①a>0时,如图1,

将x=0代入抛物线得y=-3a,
∵抛物线与线段BC恰有一个公共点,
∴-3a<1,
解得a>-![]() ,
,
将x=5代入抛物线得y=12a,
∴12a≥1,
解得a≥ ![]() ,
,
∴a≥![]() ;
;
②a<0时,如图2,

将x=0代入抛物线得y=-3a,
∵抛物线与线段BC恰有一个公共点,
∴-3a>1,
∴a<-![]() ;
;
③当抛物线的顶点在线段BC上时,则顶点为(1,1),如图3,

将点(1,1)代入抛物线得1=a-2a-3a,
解得a=-![]() .
.
综上所述,a≥![]() 或a<-
或a<-![]() 或a=-
或a=-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交,其顶点坐标为
轴正半轴相交,其顶点坐标为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根,其中正确的结论是________.(只填序号即可).
有两个相等的实数根,其中正确的结论是________.(只填序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=∠C=36°,AD、AE三等分∠A,D、E在BC边上,则其中的相似三角形(不包含全等)有( )
A.1对B.2对C.3对D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() .回答下列问题:
.回答下列问题:
(1)求出它的图像与坐标轴的交点坐标;
(2)当自变量![]() 满足什么条件时?函数值
满足什么条件时?函数值![]() ?
?
(3)当自变量![]() 时,则函数值
时,则函数值![]() 的范围?
的范围?
(4)在所给的直角坐标系中,画出直线![]() 的图像.
的图像.
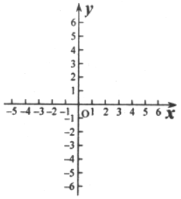
查看答案和解析>>
科目:初中数学 来源: 题型:
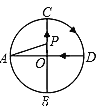
【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是 ( )
A. 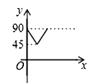 B.
B. 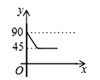 C.
C. 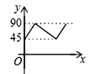 D.
D. 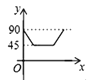
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛及周边岛屿自古以来就是中国的领土.如图,我海监飞机在距海平面高度为2千米的C处测得钓鱼岛南北两端A、B的俯角∠DCA=45°、∠DCB=30°(已知A、B、C三点在同一平面上),求钓鱼岛南北两端A、B的距离.(参考数据: ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
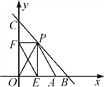
【题目】如图,直线y=-x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=-x+10在第一象限内的一个动点.
(1)求△OPA的面积S与x的函数解析式,并写出自变量x的取值范围;
(2)过点P作PE⊥x轴于点E,作PF⊥y轴于点F,连接EF,是否存在一点P使得EF的长最小,若存在,求出EF的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
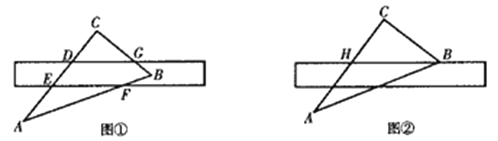
【题目】(6分)如图①所示,将直尺摆放在三角板ABC上,使直尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°。
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示.点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com