

 b×btan∠AOB-
b×btan∠AOB- a×atan∠AOB=
a×atan∠AOB=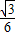 (b2-a2),
(b2-a2), (32-12)=
(32-12)=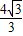 ;
;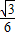 (80352-80332)=5356
(80352-80332)=5356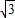 .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源:2011年北京市解密预测中考模拟试卷05(解析版) 题型:解答题
 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y= (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.
查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前30天冲刺得分专练8:二次函数(解析版) 题型:解答题
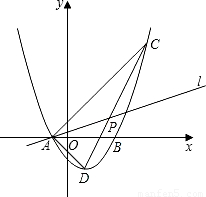
查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前30天冲刺得分专练6:函数、一次函数(解析版) 题型:解答题
 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y= (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.
查看答案和解析>>
科目:初中数学 来源:2010年浙江省宁波市南三县初中毕业生学业诊断性考试数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年四川省乐山市中考数学试卷(解析版) 题型:解答题
 x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=
x-2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y= (x<0)的图象于点Q,且tan∠AOQ=
(x<0)的图象于点Q,且tan∠AOQ= .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com