
����Ŀ����֪�� �� 2 ��![]() �ͳ��� 1 ��
�ͳ��� 1 ��![]() �ͳ���������һ�ο��˻� 10 �֣� �� 1 ��
�ͳ���������һ�ο��˻� 10 �֣� �� 1 ��![]() �ͳ��� 2 ��
�ͳ��� 2 ��![]() �ͳ���������һ�ο��˻� 11 �� �� ����������Ϣ�� ����������⣺
�ͳ���������һ�ο��˻� 11 �� �� ����������Ϣ�� ����������⣺
��1�� 1 ��![]() �ͳ��� 1 ��
�ͳ��� 1 ��![]() �ͳ���������һ�οɷֱ��˻����ٶ֣�
�ͳ���������һ�οɷֱ��˻����ٶ֣�
��2�� ij������˾���л������ɶ�Ҫ���䣬 �ƻ�ͬʱ����![]() �ͳ� 6 ����
�ͳ� 6 ����![]() �ͳ� 8 ���� һ�����꣬ ��ǡ��ÿ���������ػ�� �������������˾�ж��ٶֻ���Ҫ���䣿
�ͳ� 8 ���� һ�����꣬ ��ǡ��ÿ���������ػ�� �������������˾�ж��ٶֻ���Ҫ���䣿
���𰸡�(1)A�ͳ�3�֣�B�ͳ�4�֣�(2) 50 ��.
��������
��1����������2��A�ͳ���1��B�ͳ���������һ�ο��˻�10�֣�������1��A�ͳ���2��B�ͳ���������һ�ο��˻�11�������ó�������⼴�ɣ�
��2�����˻���=A�ͳ����˻���+B�ͳ����˻��
�⣺��1����1��![]() �ͳ���������һ�ο��˻�
�ͳ���������һ�ο��˻�![]() �֣� ��1��
�֣� ��1��![]() �ͳ���������һ�ο��˻�
�ͳ���������һ�ο��˻�![]() �֣�
�֣�
��������ã�![]() ��
��
��ã�![]() ��
��
![]() ��
��
��1��A�ͳ���������һ�ο��˻�3�֣�1��B�ͳ���������һ�ο��˻�4�� ��
��2���������������Ϊ![]() ����
����![]() ��
��
�𣺸�������˾��50�ֻ���Ҫ���� ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��֪һ�κ���y=��x+b�뷴��������y= ![]() ��ͼ����2�������㣬��b��ȡֵ��Χ�ǣ� ��
��ͼ����2�������㣬��b��ȡֵ��Χ�ǣ� ��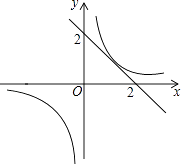
A.b��2
B.��2��b��2
C.b��2��b����2
D.b����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����ͼ![]() ����
����![]() ��
��![]() ��
��![]() �ڵ�D����֪��
�ڵ�D����֪��![]() ����Ҫ֤��
����Ҫ֤��![]() ��
��
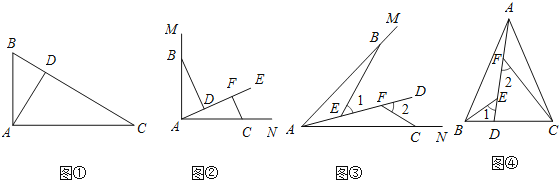
![]() ����̽������ͼ
����̽������ͼ![]() ��
��![]() ������AE������ǵ��ڲ�����B��C��
������AE������ǵ��ڲ�����B��C��![]() �ı�AM��AN�ϣ���
�ı�AM��AN�ϣ���![]() ��
��![]() �ڵ�F��
�ڵ�F��![]() �ڵ�
�ڵ�![]() ֤����
֤����![]() ��
��![]() ��
��
![]() ����֤������ͼ
����֤������ͼ![]() ����B��C��
����B��C��![]() �ı�AM��AN�ϣ���E��F��
�ı�AM��AN�ϣ���E��F��![]() �ڲ�������AD�ϣ�
�ڲ�������AD�ϣ�![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �����
�����![]() ��֪
��֪![]() ��
��![]() ��֤��
��֤��![]() ��
��![]() ��
��
![]() ��չӦ�ã���ͼ
��չӦ�ã���ͼ![]() ����
����![]() ��
��![]() ��
��![]() ��D�ڱ�BC�ϣ�
��D�ڱ�BC�ϣ�![]() ����E��F���߶�AD�ϣ�
����E��F���߶�AD�ϣ�![]() ��
��![]() �����Ϊ24����
�����Ϊ24����![]() ��
��![]() �����֮��Ϊ______
�����֮��Ϊ______![]() ֱ��д�����
ֱ��д�����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����A��3��0����B��0��4������C�ڵ�һ���ޣ�AB��BC��BC=BA����P���߶�OB�ϣ�OP=OA��AP���ӳ�����CB���ӳ��߽��ڵ�M��AB��CP���ڵ�N��

��1����C������������������
��2����֤��BM=BN��
��3�����C����ֱ��AB�ĶԳƵ�ΪD����C����ֱ��AP�ĶԳƵ�ΪG����֤��D��G����x��Գƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��ײ�,��ÿ��
��ײ�,��ÿ��![]() ǧ��Ϊ��,��������ķֱ�������������ʾ,��¼���£�
ǧ��Ϊ��,��������ķֱ�������������ʾ,��¼���£�
��������IJ� |
|
|
|
|
|
|
�� �� |
|
|
|
|
|
|
(1)��������Ƚ�,![]() ��ײ��ܼƳ����������ǧ�ˣ�
��ײ��ܼƳ����������ǧ�ˣ�
(2)���ײ�ÿǧ���ۼ�![]() Ԫ,�������
Ԫ,�������![]() ��ײ˿�������Ԫ��
��ײ˿�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ı���ABCD�У�M��N��P��Q�ֱ���AB��BC��CD��DA�ϵĵ㣬�����ı���MNPQ����״�����½����У��������![]() ����
����![]()
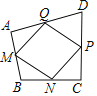
A. ��M��N��P��Q�Ǹ����е㣬�ı�MNPQһ��Ϊƽ���ı���
B. ��M��N��P��Q�Ǹ����е㣬��![]() ʱ���ı���MNPQΪ������
ʱ���ı���MNPQΪ������
C. ��M��N��P��Q�Ǹ����е㣬��![]() ʱ���ı���MNPQΪ����
ʱ���ı���MNPQΪ����
D. ��M��N��P��Q�Ǹ����е㣬��![]() ʱ���ı���MNPQΪ����
ʱ���ı���MNPQΪ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��x�ύ�ڵ�
��x�ύ�ڵ�![]() ����y�ύ�ڵ�
����y�ύ�ڵ�![]() ����ֱ��
����ֱ��![]() ��x��ĸ�����ƽ��6����λ�õ�ֱ��
��x��ĸ�����ƽ��6����λ�õ�ֱ��![]() ��ֱ��
��ֱ��![]() ��x�ύ�ڵ�C����y�ύ�ڵ�D������BC��
��x�ύ�ڵ�C����y�ύ�ڵ�D������BC��
![]() ��ͼ
��ͼ![]() ���ֱ����ֱ��
���ֱ����ֱ��![]() ��
��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
![]() �����P�ǵ�һ������ֱ��
�����P�ǵ�һ������ֱ��![]() ��һ�㣬���ı���DCBP��ƽ���ı���ʱ�����P�����ꣻ
��һ�㣬���ı���DCBP��ƽ���ı���ʱ�����P�����ꣻ
![]() ��ͼ
��ͼ![]() �������E���߶�OC���е㣬
�������E���߶�OC���е㣬![]() ����ֱ��
����ֱ��![]() �ڵ�F����y������������ܷ��ҵ�һ��M��ʹ
�ڵ�F����y������������ܷ��ҵ�һ��M��ʹ![]() �ǵ��������Σ�����ܣ���������з��������ĵ�M�����ꣻ������ܣ���˵�����ɣ�
�ǵ��������Σ�����ܣ���������з��������ĵ�M�����ꣻ������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���C������Ϊ��4����1����

��1����������ABC��CΪ��ת���ģ���˳ʱ�뷽����ת90�����ͼ����A1B1C��
��2����ԭ��OΪ�Գ����ģ��ٻ�������ABC����ԭ��O�ԳƵ���A2B2C2����д����C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߳�Ϊ4cm��������ABCD�У���P��Qͬʱ�ӵ�A����������ͬ���ٶȷֱ���A��B��C��A��D��C��·���˶�����PQ![]() cmʱ����C��PQ�ľ���Ϊ______��
cmʱ����C��PQ�ľ���Ϊ______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com