
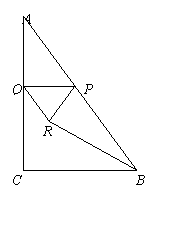
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=10,P是AB边上的一个动点(异于A、B两点),过点P作PQ⊥AC于Q,以PQ为边向下作等边三角形PQR.设AP=![]() ,△PQR与△ABC重叠部分的面积为
,△PQR与△ABC重叠部分的面积为![]() ,连接RB.
,连接RB.
(1)当![]() =2时,求
=2时,求![]() 的值;
的值;
(2)当![]() 取何值时,四边形AQRB是等腰梯形;当
取何值时,四边形AQRB是等腰梯形;当![]() 取何值时,四边形AQRB是平行四边形.
取何值时,四边形AQRB是平行四边形.
 |
解:(1)∵∠A=30°,∠AQP=90°, ∴QP=![]() AP=1.
AP=1.
此时△PQR在△ABC内,y=S△PQR=![]() . …………………………………………3分
. …………………………………………3分
(2)∵四边形AQRB是等腰梯形,∴BR=AQ, ∠PBR=∠A=30°.
∵∠APQ=∠RPQ=60°, ∴∠BPR=60°.
又∵PR=PQ, ∴△BPR≌△APQ.
∴BP=AP=![]() .∴AP=
.∴AP=![]() =5.
=5.
∴当![]() =5时,四边形AQRB是等腰梯形. …………………………………………6分
=5时,四边形AQRB是等腰梯形. …………………………………………6分
要使四边形PQRB是平行四边形,则R应在BC上.
∵△![]() PQR是等边三角形,∴QR=PQ=
PQR是等边三角形,∴QR=PQ=![]() .
.
又∵四边形PQRB是平行四边形,∴BP=QR=![]() .
.
∴AB=![]() +
+![]() =10,解得
=10,解得![]() .
.
∴当![]() 时,四边形PQRB是平行四边形.……………………………………10分
时,四边形PQRB是平行四边形.……………………………………10分
【相关知识点】直角三角形的性质;平行四边形的性质;等腰梯形的性质;全等三角形的判定与性质;等边三角形的性质;一元一次方程
【解题思路】本题是一道综合题,涉及的知识点比较多.第(1)问比较简单,根据在直角三角形中,30°的角所对的直角边等于斜边的一半可以直接求出![]() 的值;第(2)问从特殊四边形的结论出发,去找
的值;第(2)问从特殊四边形的结论出发,去找![]() 的取值,用到了等腰梯形的性质,三角形全等的判定与性质,平行四边形的性质以及方程等知识.
的取值,用到了等腰梯形的性质,三角形全等的判定与性质,平行四边形的性质以及方程等知识.


科目:初中数学 来源: 题型:
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com