练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠C=90°，∠B=60°，内切圆O与边AB、BC、CA分别相切于点D、E、F，则∠DEF的度数为°．

    【答案】75
    【解析】解：连接DO，FO，
    ∵在Rt△ABC中，∠C=90°，∠B=60°
    ∴∠A=30°，
    ∵内切圆O与边AB、BC、CA分别相切于点D、E、F，
    ∴∠ODA=∠OFA=90°，
    ∴∠DOF=150°，
    ∴∠DEF的度数为75°．
    所以答案是：75．
    【考点精析】掌握圆周角定理和三角形的内切圆与内心是解答本题的根本，需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；三角形的内切圆的圆心是三角形的三条内角平分线的交点，它叫做三角形的内心．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】学校开展的“书香校园”活动受到同学们的广泛关注，为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计图表．

    学生借阅图书的次数统计表：

    借阅图书的次数

    次

    次

    次

    次

    次及以上

    人数

    请你根据统计图表中的信息，解答下列问题：

    （1） ， ；

    （2）该调查统计数据的中位数是 ，众数是 ；

    （3）若该校共有名学生，根据调查结果，估计该校学生在一周内借阅图书次及以上的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，点P是Rt△ABC斜边AB上一动点（不与A、B重合），分别过A、B向直线CP作垂线，垂足分别为E、F、Q为斜边AB的中点．
    （1）如图1，当点P与点Q重合时，AE与BF的位置关系，QE与QF的数量关系.
    （2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；
    （3）如图3，当点P在线段BA（或AB）的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．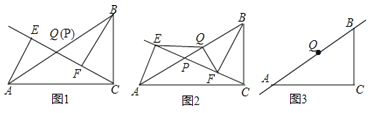

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，△ABC的三个顶点的位置如图所示，点A′的坐标是（﹣2，2），现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．

    （1）请画出平移后的△A′B′C′（不写画法）；

    （2）并直接写出点B′、C′的坐标：B′（　 　）、C′（　 　）；

    （3）若△ABC内部一点P的坐标为（a，b），则点P的对应点P′的坐标是（　 　 ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，O是AB上一点，⊙O与BC相切于点E，交AB于点F，连接AE，若AF=2BF，则∠CAE的度数是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的证明

    如图，端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点，已知∠PBA=∠PDC，∠l=∠PCD，求证：∠2+∠3=180°．

    证明：∵∠PBA=∠PDC（　 　）

    ∴　 　（同位角相等，两直线平行）

    ∴∠PAB=∠PCD（　 　）

    ∵∠1=∠PCD（　 　）

    ∴　 　（等量代换）

    ∴PC//BF（内错角相等，两直线平行），

    ∴∠AFB=∠2（　 　）

    ∵∠AFB+∠3=180°（　 　）

    ∴∠2+∠3=180°（等量代换）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知直线PQ∥MN，点A、B分别在直线MN、PQ上，射线AM绕点A以5°/秒的速度按顺时针开始旋转，旋转至与AN（或AM）重合后便立即回转，射线BQ绕点B以2°/秒的速度按顺时针开始旋转，旋转至与BP重合后便停止转动，旋转后的射线分别记为AM'和BQ'．

    （1）若射线BQ先转动30秒，射线AM才开始转动，在射线AM第一次到达AN之前，射线AM转动几秒后AM'∥BQ'；

    （2）若射线AM，BQ同时转动t秒，在射线BQ停止转动之前，记射线AM'与BQ'交于点H，若∠AHB＝90°，求t的值；

    （3）射线AM，BQ同时转动，在射线AM第一次到达AN之前，记射线AM'与BQ'交于点K，过K作KC⊥AK交PQ于点C，如图2，若∠BAN＝30°，则在旋转过程中，∠BAK与∠BKC有何数量关系？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆轿车从甲城驶往乙城，同时一辆卡车从乙城驶往甲城，两车沿相同路线匀速行驶，轿车到达乙城停留一段时间后，按原路原速返回甲城；卡车到达甲城比轿车返回甲城早0.5小时，轿车比卡车每小时多行驶60千米，两车到达甲城弧均停止行驶，两车之间的路程y（千米）与轿车行驶时间t（小时）的函数图象如图所示，请结合图象提供的信息解答下列问题：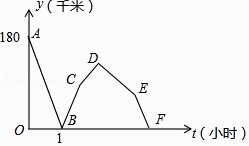
    （1）请直接写出甲城和乙城之间的路程，并求出轿车和卡车的速度；
    （2）求轿车在乙城停留的时间，并直接写出点D的坐标；
    （3）请直接写出轿车从乙城返回甲城过程中离甲城的路程s（千米）与轿车行驶时间t（小时）之间的函数关系式（不要求写出自变量的取值范围）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（c，m），则点E的坐标是（ ）
    A.（2，﹣3）
    B.（2，3）
    C.（3，2）
    D.（3，﹣2）

    查看答案和解析>>

    同步练习册答案