
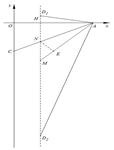
如图,已知在平面直角坐标系xOy中,抛物线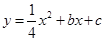 与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
(1)求这条抛物线的表达式及顶点M的坐标;
(2)求 的值;
的值;
(3)如果点D在这条抛物线的对称轴上,且∠CAD=45º,求点D的坐标.
(1)M(2,4);(2)tan∠MAC=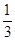 ;(3)
;(3)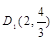 ,
,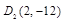 .
.
解析试题分析:
(1)根据与y轴的交点C的坐标(0,-3)就可以求出OC的值及c的值,进而求出OA的值及A的坐标,由待定系数法就可以求出b的值而求出解析式及定点坐标;
(2)如图1,过点M作MH⊥x轴,垂足为点H,交AC于点N,过点N作NE⊥AM于点E,垂足为点E.在Rt△AHM中,HM=AH=4,就可以求出AM的值,再由待定系数法求出直线AC的解析式,就可以求出点N的坐标,进而求出MN的值,由勾股定理就可以求出ME及NE的值,从而求出AE的值就可以得出结论;
(3)如图2,分类讨论,当D点在AC上方时,根据角之间的关系就可以求出∠D1AH=∠CAM,当D点在AC下方时,∠MAC=∠AD2M就可以求出点D的坐标. 试题解析:
试题解析:
∵C(0,-3),∴OC=3.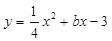
∵OA=2OC,∴OA=6.
∵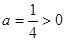 ,点A在点B右侧,抛物线与y轴交点C(0,-3)
,点A在点B右侧,抛物线与y轴交点C(0,-3)
∴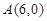 .
.
∴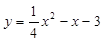 .
.
∴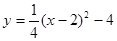 ,∴
,∴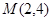 .
.
(2)过点M作MH⊥x轴,垂足为点H,交AC于点N,过点N作NE⊥AM于点E,垂足为点E.
在Rt△AHM中,HM=AH=4,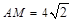 ,
,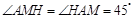 .求得直线AC的表达式为
.求得直线AC的表达式为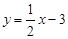 .
.
∴N(2,-2).∴MN=2.
在Rt△MNE中,∴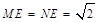 ,
,
∴ .
.
在Rt△AEN中, .
.
(3)?当D点在AC上方时,
∵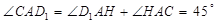 ,
,
又 ∵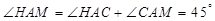 ,
,
∴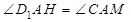 .
.
∴
∵点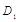 在抛物线的对称轴直线x=2上,
在抛物线的对称轴直线x=2上,
∴ ,∴
,∴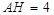 .
.
在Rt△AH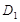 中,
中, .
.
∴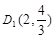 .
.
?当D点在AC下方时,
∵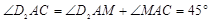 ,
,
又 ∵∠AMH=∠D2AM+∠AD2M=45º,
∴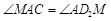 .
.
∴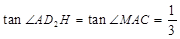
在Rt△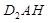 中,
中,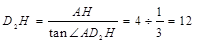 .
.
∴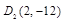 .
.
综上所述: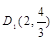 ,
,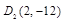 .
.
考点:二次函数综合题.


科目:初中数学 来源: 题型:计算题
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量 箱与销售价
箱与销售价 元/箱之间的函数关系式.
元/箱之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价 (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商店销售一种商品,每件的进价为2.5元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量为500件,而单价每降低1元,就可以多售出200件.请你分析,销售单价多少时,可以获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=x2+bx+c的顶点坐标为M(0,﹣1),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)判断△MAB的形状,并说明理由;
(3)过原点的任意直线(不与y轴重合)交抛物线于C、D两点,连接MC,MD,试判断MC、MD是否垂直,并说明理由.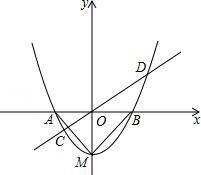
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,二次函数y=ax2+bx(a<0)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为﹣1,AC:BC=3:1.
(1)求点A的坐标;
(2)设二次函数图象的顶点为F,其对称轴与直线AB及x轴分别交于点D和点E,若△FCD与△AED相似,求此二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
锐角 中,
中, ,
, ,两动点
,两动点 分别在边
分别在边 上滑动,且
上滑动,且 ,以
,以 为边向下作正方形
为边向下作正方形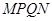 ,设其边长为
,设其边长为 ,正方形
,正方形 与
与 公共部分的面积为
公共部分的面积为 .
.
(1) 中边
中边 上高
上高 ;
;
(2)当 时,
时, 恰好落在边
恰好落在边 上(如图1);
上(如图1);
(3)当 在
在 外部时(如图2),求
外部时(如图2),求 关于
关于 的函数关系式(注明
的函数关系式(注明 的取值范围),并求出
的取值范围),并求出 为何值时
为何值时 最大,最大值是多少?
最大,最大值是多少? 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=- x2+
x2+ x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
(1)求点B,C所在直线的函数解析式;
(2)求△BCF的面积;
(3)在线段BC上是否存在点P,使得以点P,A,B为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 经过A
经过A 、C(0,4)两点,与x轴的另一交点是B.
、C(0,4)两点,与x轴的另一交点是B.
(1)求抛物线的解析式;
(2)若点 在第一象限的抛物线上,求点D关于直线BC的对称点
在第一象限的抛物线上,求点D关于直线BC的对称点 的坐标;
的坐标;
(3)在(2)的条件下,过点D作DE⊥BC于点E,反比例函数 的图象经过点E,点
的图象经过点E,点 在此反比例函数图象上,求
在此反比例函数图象上,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com