
【题目】如图,在ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.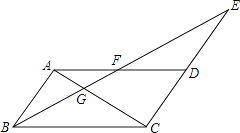
(1)求证:AF=DF;
(2)若BC=2AB,DE=1,∠ABC=60°,求FG的长.
【答案】
(1)
证明:连接BD、AE,

∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵DE=CD,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形,
∴AF=DF.
(2)
解:在BC上截取BN=AB=1,连接AN,

∵∠ABC=60°,
∴△ANB是等边三角形,
∴AN=1=BN,∠ANB=∠BAN=60°,
∵BC=2AB=2,
∴CN=1=AN,
∴∠ACN=∠CAN= ![]() ×60°=30°,
×60°=30°,
∴∠BAC=90°,
由勾股定理得:AC= ![]() =
= ![]() ,
,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△AGB∽△CGE,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
AG= ![]() ,
,
在△BGA中,由勾股定理得:BG= ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴GE= ![]() ,
,
BE= ![]() +
+ ![]() =2
=2 ![]() ,
,
∵四边形ABDE是平行四边形,
∴BF= ![]() BE=
BE= ![]() ,
,
∴FG= ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)连接AE、BD、根据AB∥CD,AB=CD=DE,得出平行四边形ABDE,即可推出答案;(2)在BC上截取BN=AB=1,连接AN,推出△ANB是等边三角形,求出CN=1=AN,根据三角形的内角和定理求出∠BAC=90°,由勾股定理求出AC,根据△AGB∽△CGE,得出 ![]() ,求出AG,在△BGA中,由勾股定理求出BG,求出GE、BE,根据平行四边形BDEA求出BF,即可求出答案.
,求出AG,在△BGA中,由勾股定理求出BG,求出GE、BE,根据平行四边形BDEA求出BF,即可求出答案.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三的一半,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,AC为⊙O的直径,PO交于⊙O于点E. 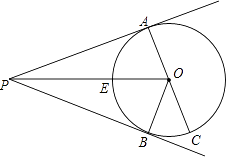
(1)试判断∠APB与∠BAC的数量关系;
(2)若⊙O的半径为4,P是⊙O外一动点,是否存在点P,使四边形PAOB为正方形?若存在,请求出PO的长,并判断点P的个数及其满足的条件;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是
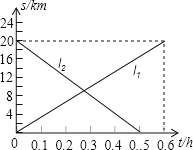
A. 乙摩托车的速度较快
B. 经过0.3小时甲摩托车行驶到A,B两地的中点
C. 经过0.25小时两摩托车相遇
D. 当乙摩托车到达A地时,甲摩托车距离A地![]() km
km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与计算
(1)已知:![]() .
.
求作:在图2中,以OA为一边,在∠AOB的内部作.∠AOC=![]() (要求:直尺和圆规作图,不写作法,保留图痕迹.)
(要求:直尺和圆规作图,不写作法,保留图痕迹.)

(2)过点O分别引射线OA、OB、OC,且∠AOB=65°,∠BOC=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a= ![]() .其中正确的是( )
.其中正确的是( )
A.②④
B.②③
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
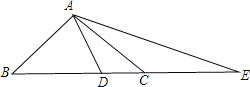
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com