
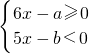 的整数解只有1和2,求适合这个不等式组的整数a与b的值.
的整数解只有1和2,求适合这个不等式组的整数a与b的值.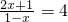 的解相同,求2x2-kx+1=0的另一个解.
的解相同,求2x2-kx+1=0的另一个解.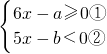
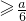 ,
, ,
, ≤1,即a取1,2,3,4,5,6六个整数;
≤1,即a取1,2,3,4,5,6六个整数; ≤3,即b取11,12,13,14,15五个整数.
≤3,即b取11,12,13,14,15五个整数.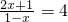 ,解得x=0.5,
,解得x=0.5, ,
, 即可求得另一根.
即可求得另一根. ,
, 的范围,是解决本题的关键.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.同时考查方程解的意义,及同解方程、解方程等知识.注意运用根与系数的关系使运算简便.
的范围,是解决本题的关键.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.同时考查方程解的意义,及同解方程、解方程等知识.注意运用根与系数的关系使运算简便. 

科目:初中数学 来源:2014届江苏省扬州市江都区八年级下学期期末考试数学试卷(解析版) 题型:选择题
如果不等式组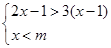 的解集是x<2,那么m的取值范围是
的解集是x<2,那么m的取值范围是
A.m="2" B.m>2 C.m<2 D.m≥2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com