
【题目】平面直角坐标系![]() 中,横坐标为a的点 A在反比例函数
中,横坐标为a的点 A在反比例函数![]() 的图象上,点
的图象上,点![]() 与点
与点![]() 关于点
关于点![]() 对称,一次函数
对称,一次函数![]() 的图象经过点
的图象经过点![]()
(1)设![]() ,点
,点![]() (4,2)在函数
(4,2)在函数![]() ,
,![]() 的图像上.
的图像上.
①分别求函数![]() ,
,![]() 的表达式;
的表达式;
②直接写出使![]() 成立的
成立的![]() 的范围;
的范围;
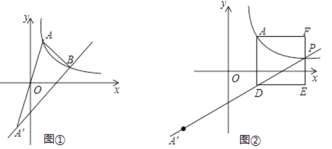
(2)如图①,设函数![]() ,
,![]() 的图像相交于点
的图像相交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,△
,△![]() 的面积为16,求
的面积为16,求![]() 的值;
的值;
(3)设![]() ,如图②,过点
,如图②,过点![]() 作
作![]() 轴,与函数
轴,与函数![]() 的图像相交于点
的图像相交于点![]() ,以
,以![]() 为一边向右侧作正方形
为一边向右侧作正方形![]() ,试说明函数
,试说明函数![]() 的图像与线段
的图像与线段![]() 的交点
的交点![]() 一定在函数
一定在函数![]() 的图像上.
的图像上.
【答案】(1)①![]() ;②2<x<4;(2)k=6;(3)见解析.
;②2<x<4;(2)k=6;(3)见解析.
【解析】
(1)由已知代入点坐标即可;
(2)面积问题可以转化为△AOB面积,用a、k表示面积问题可解;
(3)设出点A、A′坐标,依次表示AD、AF及点P坐标.
(1)解:∵点B(4,2) 在函数![]() ,
,![]() 的图像上.∴k=4×2=8∴
的图像上.∴k=4×2=8∴![]()
∵点A在![]() 上∴x=a=2,y=4∴点A(2,4)
上∴x=a=2,y=4∴点A(2,4)
∵A和点A'关于原点对称
∴点A'的坐标为(-2,-4)
∵一次函数y2=mx+n的图像经过点A'和点B![]()
解得:![]() ∴y2=x-2;
∴y2=x-2;
②由图像可知,当![]() 时,y1=
时,y1=![]() 图象在y2=x-2图象上方,且两函数图象在x轴上方,
图象在y2=x-2图象上方,且两函数图象在x轴上方,
∴由图象得: 2<x<4;
(2)解:)分别过点A、B作AC⊥x轴于点C,BD⊥x轴于点D,连BO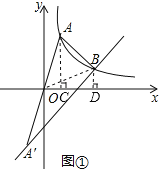
∵O为AA′中点
S△AOB=![]() S△ABA′=8
S△ABA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为(a,![]() )(3a,
)(3a,![]() )
)
∴![]() ×(
×(![]() +
+![]() )×2a=8
)×2a=8
解得k=6;
(3)解:设A(a ,![]() ),则A′(﹣a ,﹣
),则A′(﹣a ,﹣![]() ),代入
),代入![]() 得
得 ![]() ,
,
∴![]() ,
,
∴D(a,![]() )
)
∴AD=![]() ,
,
∵AD=AF,
∴![]() ,代入
,代入![]() 得
得![]() ,即P(
,即P(![]() ,
,![]() )
)
将点P横坐标代入![]() 得纵坐标为
得纵坐标为![]() ,可见点P一定在函数
,可见点P一定在函数![]() 的图像上.
的图像上.
故答案为(1)①![]() ;②2<x<4;(2)k=6;(3)见解析.
;②2<x<4;(2)k=6;(3)见解析.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,以AC为底边作等腰△ACD,且使∠ABC=2∠CAD,连接BD.

(1)如图1,若∠ADC=90°,∠BAC=30°,BC=1,求CD的长;
(2)如图1,若∠ADC=90°,证明:AB+BC=![]() BD;
BD;
(3)如图2,若∠ADC=60°,探究AB,BC,BD之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
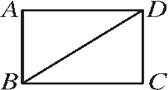
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4,AB=12.
(1)求点A、B对应的数;
(2)动点P、Q分别同时从A、C出发,分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且CN=![]() CQ,设运动时间为t(t>0).
CQ,设运动时间为t(t>0).
①求点M、N对应的数(用含t的式子表示); ②t为何值时,OM=2BN.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
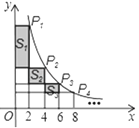
【题目】如图,在函数y=![]() (x>0)的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn,则Sn=______.(用含n的代数式表示)
(x>0)的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn,则Sn=______.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】恰逢“植树节”,师梅与博小两所学校决定购进A,B两种树苗进行种植,已知两所学校共花费了390元购进了50棵树苗,其中A树苗10元一棵,B树苗5元一棵.现在要将50棵树苗运往两所学校,其运费如下表所示:
树苗类型 | 师梅(元/棵) | 博小(元/棵) |
A | 8 | 10 |
B | 6 | 5 |
(1)求这50棵树苗中A、B树苗各多少棵?
(2)现师梅需要30棵树苗,博小需要20棵树苗,设师梅需要A树苗为x棵,运往师梅和博小的总运费为y,求y与x的函数解析式.
(3)在(2)的条件下,若运往师梅的运费不超过200元,请你写出使总运费最少的树苗分配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B. 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
C. “明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D. 了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com