能否将1,2,3…,12这12个正整数分成两组,使得其中第一组有3个数,第二组有9个数,并且第一组中3个数的积恰好等于第二组中9个数之和?若能,请给出所有的分组方法;若不能,请说明理由.
分析:设第一组中的三个数为a、b、c(a<b<c),然后可得出第二组中九个数的和为:
×12×13-(a+b+c)=78-(a+b+c),从而得出abc+a+b+c=78,结合a<b<c可得出a的范围,分别讨论a的值即可得出可能的答案.
解答:解:设第一组中的三个数为a、b、c(a<b<c),则第二组中九个数的和为:
×12×13-(a+b+c)=78-(a+b+c).
∴abc+a+b+c=78①,
由a<b<c及①得:a
3+3a+3<78,
解得:0<a<4,
当a=1时,由①得bc+b+c+1=(b+1)(c+1)=78=6×13,
解得a=1,b=5,c=12,
当a=2时,由①得2bc+b+c+2=(2b+1)(2c+1)=9×17,
解得a=2,b=4,c=8,
当a=2时,由①得3bc+b+c+3=78,即(3b+1)(3c+1)=226,
此时无解.
综上所述共有两种方法:
第一种:当第一组的三个数为1,5,12时,第二组的九个数为2,3,4,6,7,8,9,10,11.
第二种:当第一组的三个数为2,4,8时,第二组的九个数为1,3,5,6,7,9,10,11,12.
点评:本题考查了整数问题的综合运用,难度较大,解答本题的关键根据题意得出a的取值范围,然后分类讨论a的取值.



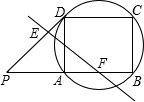 线EF能否将四边形PBCD的周长和面积同时平分?若能,请求出BF的长.若不能,请说明理由.
线EF能否将四边形PBCD的周长和面积同时平分?若能,请求出BF的长.若不能,请说明理由.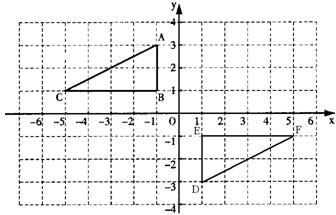 21、如图,△ABC和△DEF在平面直角坐标系中的位置如图所示.
21、如图,△ABC和△DEF在平面直角坐标系中的位置如图所示.