
【题目】已知抛物线的顶点为![]() ,且过点
,且过点![]() .直线
.直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .
.
(1)求该抛物线的解析式;
(2)以线段![]() 为直径的圆与射线
为直径的圆与射线![]() 相交于点
相交于点![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)先设出抛物线的顶点式,再将点A的坐标代入可得出结果;
(2)先求出射线![]() 的解析式为
的解析式为![]() ,可设点P的坐标为(x,x).圆与射线OA相交于两点,分两种情况:①如图1当
,可设点P的坐标为(x,x).圆与射线OA相交于两点,分两种情况:①如图1当![]() 时,构造
时,构造![]() 和
和![]() ,再在直角三角形中利用勾股定理,列方程求解;②如图2,当
,再在直角三角形中利用勾股定理,列方程求解;②如图2,当![]() 时,构造
时,构造![]() 和
和![]() ,再在直角三角形中利用勾股定理,列方程求解.
,再在直角三角形中利用勾股定理,列方程求解.
解:(1)根据顶点设抛物线的解析式为:![]() ,
,
代入点![]() ,得:
,得:![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
设直线![]() 的解析式为:
的解析式为:![]() ,
,
分别代入![]() 和
和![]() ,
,
得:![]() ,
,
直线![]() 的解析式为:
的解析式为:![]() ;
;
(2)由(1)得:直线![]() 的解析式为
的解析式为![]() ,
,
令![]() ,得
,得![]() ,
,![]()
由题意可得射线![]() 的解析式为
的解析式为![]() ,
,
![]() 点
点![]() 在射线
在射线![]() 上,则可设点
上,则可设点![]() ,
,
由图可知满足条件的点![]() 有两个:
有两个:
①当![]() 时,构造
时,构造![]() 和
和![]() ,
,
可得:如图1:
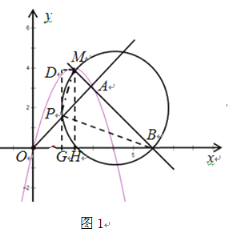
由图可得,![]() ,
,![]() ,
,
![]() .
.
在Rt△PMD中,![]() ,
,
在Rt△PBG中,![]() ,
,
在Rt△BMH中,![]() ,
,
![]() 点
点![]() 在以线段
在以线段![]() 为直径的圆上,
为直径的圆上,![]() ,
,
可得:![]() ,
,
即:![]() .
.
整理,得:
![]() ,解得:
,解得:![]() ;
;
![]() ,
,![]() .
.
![]() ;
;
②当![]() 时,如图2,构造
时,如图2,构造![]() 和
和![]() ,可得:
,可得:
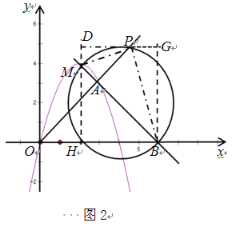
同理,根据BM2=BP2+PM2,可得方程:
42+42=(6-x)2+x2+(x-2)2+(x-4)2,化简得,
![]() ,解得:
,解得:![]() ,
,
∵![]() .
.
![]() .
.
综上所述,符合题目条件的![]() 点有两个,其坐标分别为:
点有两个,其坐标分别为:![]() 或
或![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AC=BC,∠ACB=90°,点P为AB上一点(异于A、B),BD⊥直线CP于D,AE⊥直线CP于E,点F为AB的中点,连接DF.
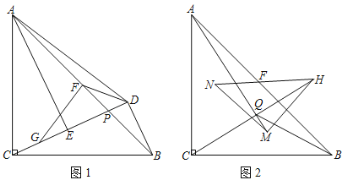
(1)可以把△ACE绕点F逆时针旋转 度(度数不超过180°)和△ 重合,则∠FDE= °.
(2)取CE的中点G,连接AD、FG,求证:AD=2FG.
(3)如图2,AB=8,等腰直角△MNH的斜边NH的中点也为点F,直线AM和直线CH交于点Q,连接BQ,当△MNH绕点F旋转一周时,请直接写出BQ长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
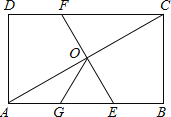
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG;(2)OG= ![]() BC;(3)△OGE是等边三角形;(4)
BC;(3)△OGE是等边三角形;(4)![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣![]() 与y轴交于点C,与x轴交于点A(﹣1,0),B(3,0).
与y轴交于点C,与x轴交于点A(﹣1,0),B(3,0).

(1)求这个抛物线的解析式;
(2)将△AOC以每秒一个单位的速度沿x轴向右平移,平移时间为t秒,平移后的△A′O′C′与△BOC重叠部分的面积为S,A与B重合时停止平移,求S与t的函数关系式;
(3)点P在x轴上,连接CP,点B关于直线CP的对称点为B′,若点B′落在这个抛物线的对称轴上,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
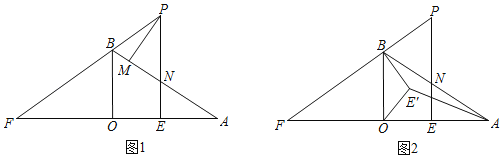
【题目】如图1,∠AOB=90°,OA=4,OB=3,点E在线段OA上,EP⊥OA交AB于点N,PM⊥AB,直线PB与AO交于点F.
(1)若AN=3,S△PBN=8,求PN的长;
(2)设△PMN的周长为C1,△AEN的周长为C2,若△PFE~△BAO且![]() =
=![]() ,求OE的长;
,求OE的长;
(3)如图2,若OE=2,将线段OE绕点O逆时针旋转得到OE',旋转角为α (0°<α<90°),连接E'A、E'B,求E'A+![]() E'B的最小值.
E'B的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场今年第一季度的产值为50万元,第二季度由于改进了生产方法,产值提高了![]() ;但在今年第三、第四季度时该农场因管理不善.导致其第四季度的产值与第二季度的产值相比下降了11.4万元.
;但在今年第三、第四季度时该农场因管理不善.导致其第四季度的产值与第二季度的产值相比下降了11.4万元.
(1)求该农场在第二季度的产值;
(2)求该农场在第三、第四季度产值的平均下降的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A(-3,0)、B(1,0),与y轴交于点C.
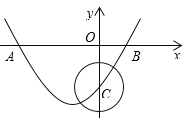
(1)求抛物线的函数表达式.
(2)在抛物线上是否存在点D,使得△ABD的面积等于△ABC的面积的![]() 倍?若存在,求出点D的坐标;若不存在,请说明理由.
倍?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点E是以点C为圆心且1为半径的圆上的动点,点F是AE的中点,请直接写出线段OF的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
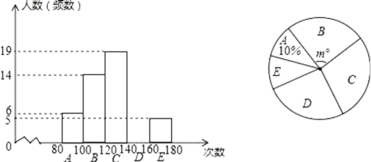
(1)补全频数分布直方图;
(2)扇形图中m= ;
(3)若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com