
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2![]() .
.
(1)利用尺规作线段AC的垂直平分线DE,垂足为E,交AB于点D;(保留作图痕迹,不写作法)
(2)若△ADE的周长为a,先化简T=(a+1)2﹣a(a﹣1),再求T的值.

【答案】(1)作图见解析(2)10+![]() .
.
【解析】分析:(1)垂直平分线的尺规作图方法:先以A为圆心,以大于线段AC一半的长度画弧,然后再以C为圆心,以相同长度为半径画弧,两条圆弧交于两点,连接该两点的直线即为线段AC的垂直平分线。(2)先化简,然后利用三角形的周长求出a,最后代入即可求得T的值。
详解:(1)如图所示,DE即为所求;
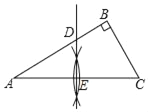
(2)由题可得,AE=![]() AC=
AC=![]() ,∠A=30°,
,∠A=30°,
∴Rt△ADE中,DE=![]() AD,
AD,
设DE=x,则AD=2x,
∴Rt△ADE中,x2+(![]() )2=(2x)2,
)2=(2x)2,
解得x=1,
∴△ADE的周长a=1+2+![]() =3+
=3+![]() ,
,
∵T=(a+1)2﹣a(a﹣1)=3a+1,
∴当a=3+![]() 时,T=3(3+
时,T=3(3+![]() )+1=10+3
)+1=10+3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
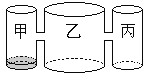
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4分别与x轴、y轴交于点A,B,双曲线![]() (k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.
(k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面内给定射线OA,射线OB及∠MON,给出如下定义:若由射线OA、OB组成的∠AOB的平分线OT落在∠MON的内部或边OM、ON上,则称射线OA与射线OB关于∠MON内含对称.例如,图1中射线OA与射线OB关于∠MON内含对称

已知:如图2,在平面内,∠AOM=10°,∠MON=20°
(1)若有两条射线![]() ,
,![]() 的位置如图3所示,且
的位置如图3所示,且![]() ,
,![]() ,则在这两条射线中,与射线OA关于∠MON内含对称的射线是_____________
,则在这两条射线中,与射线OA关于∠MON内含对称的射线是_____________
(2)射线OC是平面上绕点O旋转的一条动射线,若射线OA与射线OC关于∠MON内含对称,设∠COM=x°,求x的取值范围;
(3)如图4,∠AOE=∠EOH=2∠FOH=20°,现将射线OH绕点O以每秒1°的速度顺时针旋转,同时将射线OE和OF绕点O都以每秒3°的速度顺时针旋转.设旋转的时间为t秒,且![]() .若∠FOE的内部及两边至少存在一条以O为顶点的射线与射线OH关于∠MON内含对称,直接写出t的取值范围.
.若∠FOE的内部及两边至少存在一条以O为顶点的射线与射线OH关于∠MON内含对称,直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,

求证:(1)△AME∽△BAE;(2)BD2=AD×DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学模仿二维码的方式为学校设计了一个身份识别图案系统:在![]() 的正方形网格中,黑色正方形表示数字1,白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下:把第i行,第j列表示的数字记为
的正方形网格中,黑色正方形表示数字1,白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下:把第i行,第j列表示的数字记为![]() (其中i,j=1,2,3,4),如图1中第2行第1列的数字
(其中i,j=1,2,3,4),如图1中第2行第1列的数字![]() =0;对第i行使用公式
=0;对第i行使用公式![]() 进行计算,所得结果
进行计算,所得结果![]() 表示所在年级,
表示所在年级,![]() 表示所在班级,
表示所在班级,![]() 表示学号的十位数字,
表示学号的十位数字,![]() 表示学号的个位数字.如图1中,第二行
表示学号的个位数字.如图1中,第二行![]() ,说明这个学生在5班.
,说明这个学生在5班.
(1)图1代表的学生所在年级是______年级,他的学号是_________;
(2)请仿照图1,在图2中画出八年级4班学号是36的同学的身份识别图案

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠![]() =90°,
=90°,![]() =
=![]() =6,点
=6,点![]() 在边
在边![]() 上运动,过点
上运动,过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作□
为邻边作□![]() ,设□
,设□![]() 与△
与△![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,线段
,线段![]() 的长为
的长为![]() (0<
(0<![]() ≤6).
≤6).
(1)求线段![]() 的长(用含
的长(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落现在变
落现在变![]() 上时,求
上时,求![]() 的值;
的值;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)直接写出点![]() 到△
到△![]() 任意两边所在直线的距离相等时
任意两边所在直线的距离相等时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
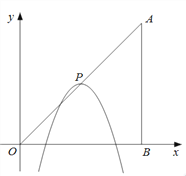
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(6,6)、(6,0).抛物线![]() 的顶点P在折线OAAB上运动.
的顶点P在折线OAAB上运动.
(1)当点P在线段OA上运动时,抛物线![]() 与y轴交点坐标为(0,c).
与y轴交点坐标为(0,c).
①用含m的代数式表示n;
②求c的取值范围;
(2)当抛物线![]() 经过点B时,求抛物线所对应的函数表达式.
经过点B时,求抛物线所对应的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com