Question

如图，AB是⊙O的直径，动弦CD垂直AB于点E，过点B作直线BF∥CD交AD的延长线于点F，若AB=10cm．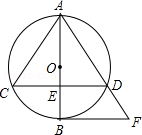

（1）求证：BF是⊙O的切线．
（2）若AD=8cm，求BE的长．
（3）若四边形CBFD为平行四边形，则四边形ACBD为何种四边形？并说明理由．

Answer 1

解：（1）证明：∵CD⊥AB，BF∥CD，∴BF⊥AB。
又∵AB是⊙O的直径，∴BF是⊙O的切线。 
（2）如图1，连接BD。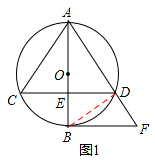

∵AB是⊙O的直径，
∴∠ADB=90°（直径所对的圆周角是直角）。
又∵DE⊥AB，∴△ADE∽△ABD。
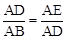∴。∴AD²=AE•AB。
∵AD=8cm，AB=10cm，∴AE=6.4cm。∴BE=AB﹣AE=3.6cm。
（3）若四边形CBFD为平行四边形，则四边形ACBD是正方形。理由如下：
连接BC。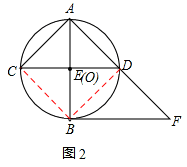

∵四边形CBFD为平行四边形，
∴BC∥FD，即BC∥AD。
∴∠BCD=∠ADC（两直线平行，内错角相等）。
∵∠BCD=∠BAD，∠CAB=∠CDB，（同弧所对的圆周角相等），
∴∠CAB+∠BAD=∠CDB+∠ADC，即∠CAD=∠BDA，
又∵∠BDA=90°（直径所对的圆周角是直角），∴∠CAD=∠BDA=90°。
∴CD是⊙O的直径，即点E与点O重合（或线段CD过圆心O）。
在△OBC和△ODA中，∵OC=OD，∠COB=∠DOA=90°，OB=OA，
∴△OBC≌△ODA（SAS）。∴BC=DA（全等三角形的对应边相等）。
∴四边形ACBD是平行四边形（对边平行且相等的四边形是平行四边形），
∵∠ACB=90°（直径所对的圆周角是直角），AC=AD，∴四边形ACBD是正方形。

解析