
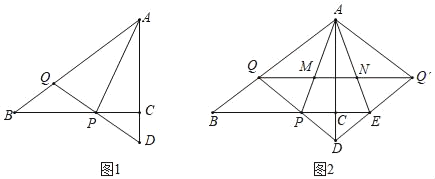
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点P在线段BC上,点Q在线段AB上,且PQ=BQ,延长QP交射线AC于点D.
(1)求证:QA=QD;
(2)设∠BAP=α,当2tanα是正整数时,求PC的长;
(3)作点Q关于AC的对称点Q′,连结QQ′,AQ′,DQ′,延长BC交线段DQ′于点E,连结AE,QQ′分别与AP,AE交于点M,N(如图2所示).若存在常数k,满足kMN=PEQQ′,求k的值.
【答案】(1)证明见解析(2)PC的长为![]() 或
或![]() (3)8
(3)8
【解析】
(1)由等腰三角形的性质得出∠B=∠BPQ=∠CPD,由直角三角形的性质得出∠BAC=∠D,即可得出结论;
(2)过点P作PH⊥AB于H,设PH=3x,BH=4x,BP=5x,由题意知tanα=1或![]() ,当tanα=1时,HA=PH=3x,与勾股定理得出3x+4x=5,解得x=
,当tanα=1时,HA=PH=3x,与勾股定理得出3x+4x=5,解得x=![]() ,即可求出PC长;
,即可求出PC长;
当tanα=![]() 时,HA=2PH﹣6x,得出6x+4x=5,解得x=
时,HA=2PH﹣6x,得出6x+4x=5,解得x=![]() ,即可求出PC长;
,即可求出PC长;
(3)设QQ′与AD交于点O,由轴对称的性质得出AQ′=AQ=DQ=DQ′,得出四边形AQDQ′是菱形,由菱形的性质得出QQ′⊥AD,AO=![]() AD,证出四边形BEQ'Q是平行四边形,得出QQ′=BE,设CD=3m,则PC=4m,AD=3+3m,即QQ′﹣BE=4m+4,PE=8m,由三角函数得出
AD,证出四边形BEQ'Q是平行四边形,得出QQ′=BE,设CD=3m,则PC=4m,AD=3+3m,即QQ′﹣BE=4m+4,PE=8m,由三角函数得出![]() =tan∠PAC=
=tan∠PAC=![]() ,即可得出结果.
,即可得出结果.
(1)证明:∵PQ=BQ,
∴∠B=∠BPQ=∠CPD,
∵∠ACB=∠PCD=90°,
∴∠A+∠BAC=90°,∠D+∠CPD=90°,
∴∠BAC=∠D,
∴QA=QD;
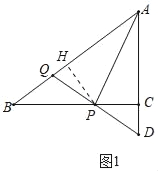
(2)解:过点P作PH⊥AB于H,如图1所示:
设PH=3x,BH=4x,BP=5x,
由题意得:tan∠BAC=![]() ,∠BAP<∠BAC,
,∠BAP<∠BAC,
∴2tanα是正整数时,tanα=1或![]() ,
,
当tanα=1时,HA=PH=3x,
∴3x+4x=![]() =5,
=5,
∴x=![]() ,
,
即PC=4﹣5x=![]() ;
;
当tanα=![]() 时,HA=2PH﹣6x,
时,HA=2PH﹣6x,
∴6x+4x=5,
∴x=![]() ,
,
即PC=4﹣5x=![]() ;
;
综上所述,PC的长为![]() 或
或![]() ;
;
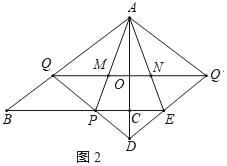
(3)解:设QQ′与AD交于点O,如图2所示:
由轴对称的性质得:AQ′=AQ=DQ=DQ′,
∴四边形AQDQ′是菱形,
∴QQ′⊥AD,AO=![]() AD,
AD,
∵BC⊥AC,
∴QQ′∥BE,
∵BQ∥EQ′,
∴四边形BEQ'Q是平行四边形,
∴QQ′=BE,
设CD=3m,则PC=4m,AD=3+3m,
即QQ′﹣BE=4m+4,PE=8m,
∵![]() =tan∠PAC=
=tan∠PAC=![]() ,
,
∴![]() =
=![]() ,
,
即MN=2MO=4m(1+m),
∴k=![]() =
=![]() =8.
=8.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() ,
,![]() 于
于![]() 点,且
点,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() ,
,![]() 于
于![]() ,且
,且![]() .
.
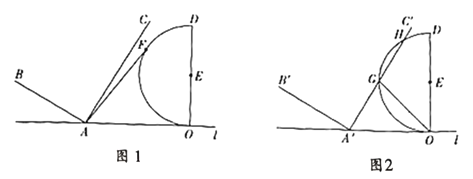
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为________;
的最大值为________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() ;
;
①如图,若![]() 截半圆
截半圆![]() 的
的![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对初三学生进行物理、化学实验操作能力测试.物理、化学各有3个不同的操作实验题目,物理实验分别用①、②、③表示,化学实验分别用a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.王刚同学对物理的①、②号实验和化学的b、c号实验准备得较好.请用画树状图(或列表)的方法,求王刚同学同时抽到两科都准备得较好的实验题目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
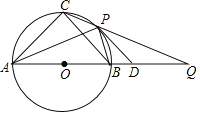
【题目】如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为![]() 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论:①若∠PAB=30°,则
上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论:①若∠PAB=30°,则![]() 的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6
的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6![]() ;④无论点P在
;④无论点P在![]() 上的位置如何变化,CPCQ为定值.其中正确的是________________.(写出所有正确结论的序号)
上的位置如何变化,CPCQ为定值.其中正确的是________________.(写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
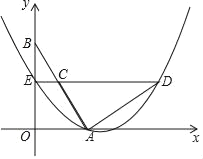
【题目】如图,两个完全相同的直角三角板放置在平面直角坐标系中,点A,B分别在x轴、y轴上,点C在边AB上,延长DC交y轴于点E.若点D的横坐标为5,∠OBA=30°,二次函数y=ax2+bx+c的图象经过点A,D,E,则a的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
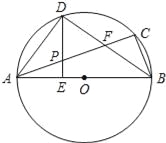
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
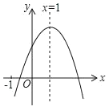
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列4个结论:①abc<0;②2a+b=0;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
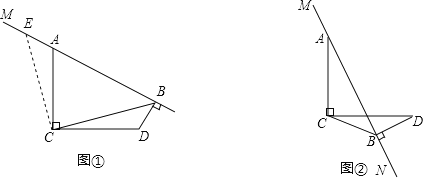
【题目】已知![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
(感知)如图①,点![]() 、
、![]() 在
在![]() 同侧,且点
同侧,且点![]() 在
在![]() 右侧,在射线
右侧,在射线![]() 上截取
上截取![]() ,连接
,连接![]() ,可证
,可证![]() ,从而得出
,从而得出![]() ,
,![]() ,进而得出
,进而得出![]() 度.
度.
(探究)如图②,当点![]() 、
、![]() 在
在![]() 异侧时,(感知)得出的
异侧时,(感知)得出的![]() 的大小是否改变?若不改变,给出证明;若改变,请求出
的大小是否改变?若不改变,给出证明;若改变,请求出![]() 的大小.
的大小.
(应用)在直线![]() 绕点
绕点![]() 旋转的过程中,当
旋转的过程中,当![]() ,
,![]() 时,直接写出
时,直接写出![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com