
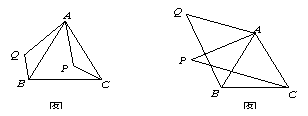
“如图①,已知在△ABC中,AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ、CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,将点P移到等腰三角形ABC之外,原题中的条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 |
| 2 |
| 9 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 .
.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com