
【题目】如图,已知在平行四边形ABCD中,点E是CD上一点,且DE=2,CE=3,射线AE与射线BC相交于点F; 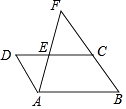
(1)求 ![]() 的值;
的值;
(2)如果 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求向量
,求向量 ![]() ;(用向量
;(用向量 ![]() 、
、 ![]() 表示)
表示)
【答案】
(1)解:∵四边形ABCD是平行四边形,DE=2,CE=3,
∴AB=DC=DE+CE=5,且AB∥EC,
∴△FEC∽△FAB,
∴ ![]() =
= ![]() =
= ![]() ;
;
(2)解:∵△FEC∽△FAB,
∴ ![]() =
= ![]() ,
,
∴FC= ![]() BC,EC=
BC,EC= ![]() AB,
AB,
∵四边形ABCD是平行四边形,
∴AD∥BC,EC∥AB,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
![]() =
= ![]()
![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() ,
,
则 ![]() =
= ![]() +
+ ![]() =
= ![]() .
.
【解析】(1)根据平行四边形的性质得出AB=5、AB∥EC,证△FEC∽△FAB得 ![]() =
= ![]() =
= ![]() ;(2)由△FEC∽△FAB得
;(2)由△FEC∽△FAB得 ![]() =
= ![]() ,从而知FC=
,从而知FC= ![]() BC,EC=
BC,EC= ![]() AB,再由平行四边形性质及向量可得
AB,再由平行四边形性质及向量可得 ![]() =
= ![]()
![]() =
= ![]()
![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() ,最后根据向量的运算得出答案.
,最后根据向量的运算得出答案.
【考点精析】掌握平行四边形的性质和相似三角形的判定与性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE= ![]() AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF= ![]() :2.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
:2.当边AD或BC所在的直线与⊙O相切时,AB的长是 . 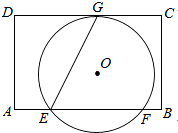
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路. 
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AECD=ADCE. 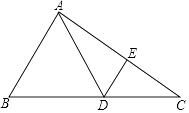
(1)求证:DE∥AB;
(2)如果点F是DE延长线上一点,且BD是DF和AB的比例中项,联结AF.求证:DF=AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是射线CB上的动点,点F是射线CD上一点,且AF⊥AE,射线EF与对角线BD交于点G,与射线AD交于点M;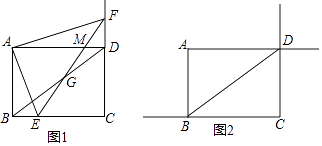
(1)当点E在线段BC上时,求证:△AEF∽△ABD;
(2)在(1)的条件下,联结AG,设BE=x,tan∠MAG=y,求y关于x的函数解析式,并写出x的取值范围;
(3)当△AGM与△ADF相似时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=5,tanA= ![]() ,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E;
,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E; 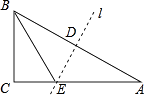
(1)求△ABC的面积;
(2)求sin∠CBE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的 ![]() O与边AB相交于点D,DE⊥AC,垂足为点E.
O与边AB相交于点D,DE⊥AC,垂足为点E. 
(1)求证:点D是AB的中点;
(2)判断DE与 ![]() O的位置关系,并证明你的结论;
O的位置关系,并证明你的结论;
(3)若 ![]() O的直径为3,cosB=
O的直径为3,cosB= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com