练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2013•宁波）7张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（　　）
    分析：表示出左上角与右下角部分的面积，求出之差，根据之差与BC无关即可求出a与b的关系式．
    解答：解：左上角阴影部分的长为AE，宽为AF=3b，右下角阴影部分的长为PC，宽为a，
    ∵AD=BC，即AE+ED=AE+a，BC=BP+PC=4b+PC，
    ∴AE+a=4b+PC，即AE-PC=4b-a，
    ∴阴影部分面积之差S=AE•AF-PC•CG=3bAE-aPC=3b（PC+4b-a）-aPC=（3b-a）PC+12b2-3ab，
    则3b-a=0，即a=3b．
    法二：既然BC是变化的，当点P与点C重合开始，然后BC向右伸展，
    设向右伸展长度为X，左上阴影增加的是3bX，右下阴影增加的是aX，因为S不变，
    ∴增加的面积相等，
    ∴3bX=aX，
    ∴a=3b．
    故选B
    点评：此题考查了整式的混合运算的应用，弄清题意是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•宁波）下列计算正确的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

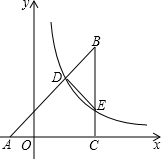    （2013•宁波）如图，等腰直角三角形ABC顶点A在x轴上，∠BCA=90°，AC=BC=2
    		2
    ，反比例函数y=
    3
    x
    （x＞0）的图象分别与AB，BC交于点D，E．连结DE，当△BDE∽△BCA时，点E的坐标为
    （
    3
    2
    		2
    ，
    		2
    ）
    （
    3
    2
    		2
    ，
    		2
    ）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•宁波）2013年5月7日浙江省11个城市的空气质量指数（AQI）如图所示：
    （1）这11个城市当天的空气质量指数的极差、众数和中位数分别是多少？
    （2）当0≤AQI≤50时，空气质量为优．求这11个城市当天的空气质量为优的频率；
    （3）求宁波、嘉兴、舟山、绍兴、台州五个城市当天的空气质量指数的平均数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

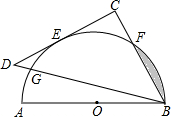    （2013•宁波模拟）如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．
    （1）求量角器在点G处的读数α（0°＜α＜90°）；
    （2）若AB=10cm，求阴影部分面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•宁波模拟）如图，在平面直角坐标系中，二次函数y=ax2+6x+c的图象经过点A（4，0）、B（-1，0），与y轴交于点C，点D在线段OC上，OD=t，点E在第二象限，∠ADE=90°，tan∠DAE=
    12
    ，EF⊥OD，垂足为F．
    （1）求这个二次函数的解析式；
    （2）求线段EF、OF的长（用含t的代数式表示）；
    （3）当△ECA为直角三角形时，求t的值．

    查看答案和解析>>

    同步练习册答案