
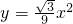 经过PR的中点M.
经过PR的中点M.
 a,
a, a,
a, a),
a), x2经过点M,
x2经过点M, (
( a)2=
a)2= a,
a, ,
, ),P(0,2
),P(0,2 ),Q(-6,0);
),Q(-6,0);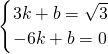 ,
,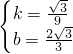 ,
, x+
x+ ;
;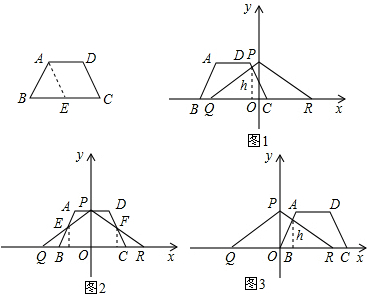
 =2
=2 ,
, h+
h+ h=CQ,
h=CQ, CQ=
CQ= t,
t, ×CQ•h=
×CQ•h= ×2t×
×2t× t=
t= t2,
t2, ×12×2
×12×2 -
- ×(2t-8)×
×(2t-8)× (8-2t)-
(8-2t)- ×(12-2t)×
×(12-2t)× (12-2t),
(12-2t), -
- (t-4)2-
(t-4)2- (6-t)2,
(6-t)2, t2+20
t2+20 t-40
t-40 ;
; BR=
BR= (10-t),
(10-t), ×(20-2t)×
×(20-2t)× (10-t),
(10-t), (10-t)2,
(10-t)2, t2-10
t2-10 t+50
t+50 ,
,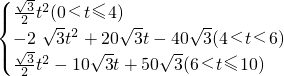 .
. a,然后根据点M是PR的中点表示出点M的坐标,再代入函数解析式求解即可;
a,然后根据点M是PR的中点表示出点M的坐标,再代入函数解析式求解即可;

科目:初中数学 来源: 题型:
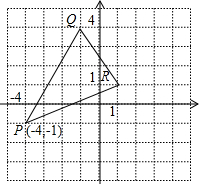 已知△PQR在直角坐标系中的位置如图所示:
已知△PQR在直角坐标系中的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 9 |
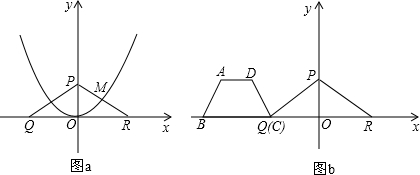
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010年湖北省襄樊市襄城区优录考试数学试卷(4月份)(解析版) 题型:解答题
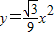 经过PR的中点M.
经过PR的中点M.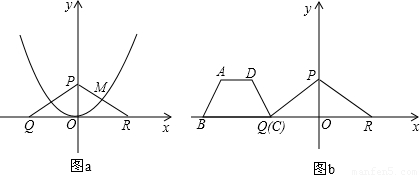
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com