
【题目】如图,抛物线![]() 与直线
与直线![]() 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为![]() 。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
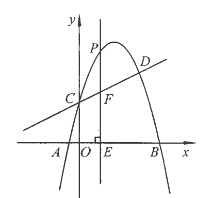
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由;
(3)若存在点P,使∠PCF=450,请直接写出相应的点P的坐标。
【答案】(1)![]() (2)平行四边形(3)P(
(2)平行四边形(3)P(![]() )或(
)或(![]() )
)
【解析】解:(1)∵直线![]() 经过点C,∴C(0,2)。
经过点C,∴C(0,2)。
∵抛物线![]() 经过点C(0,2),D
经过点C(0,2),D ![]() ,
,
∴ ,解得
,解得![]() 。
。
∴抛物线的解析式为![]() 。
。
(2)∵点P的横坐标为m且在抛物线上,
∴![]() 。
。
∵PF∥CO,∴当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形。
当![]() 时,
时,![]() ,
,
∴![]() ,解得:
,解得:![]() 。
。
即当m=1或2时,四边形OCPF是平行四边形。
当![]() 时,
时,![]() ,
,
∴![]() ,解得:
,解得:![]() (∵点P在y轴右侧的抛物线上,∴舍去)
(∵点P在y轴右侧的抛物线上,∴舍去)
即当![]() 时,四边形OCFP是平行四边形。
时,四边形OCFP是平行四边形。
综上所述,当m=1或2或![]() 时,以O,C,P,F为顶点的四边形是平行四边形。
时,以O,C,P,F为顶点的四边形是平行四边形。
(3)P(![]() )或(
)或(![]() )。
)。
(1)由直线![]() 经过点C,求出点C的坐标;由抛物线
经过点C,求出点C的坐标;由抛物线![]() 经过点C,D两点,用待定系数法即可求出抛物线的解析式。
经过点C,D两点,用待定系数法即可求出抛物线的解析式。
(2)因为PF∥CO,所以当PF=CO时,以O,C,P,F为顶点的四边形是平行四边形,分![]() 和
和![]() 两种情况讨论即可。
两种情况讨论即可。
(3)如图,当点P在CD上方且∠PCF=450时,

作PM⊥CD于点M,CN⊥PF于点N,则△PMF∽△CNF,
∴ 。∴PM=CM=2CF。
。∴PM=CM=2CF。
∴![]() 。
。
又∵![]() ,∴
,∴![]() 。
。
解得:![]() ,
,![]() (舍去)。
(舍去)。
∴P(![]() )。
)。
当点P在CD下方且∠PCF=450时,
同理可以求得:另外一点为P(![]() )。
)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为![]() 米,广场的长为
米,广场的长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示花坛的面积和广场空地的面积;
(2)若休闲广场的长为500米,宽为200米,圆形花坛的半径为20米,求广场空地的面积;(计算结果保留![]() ;
;
(3)在(2)的情况下,若![]() 取3.14,求休闲广场的绿化率是多少?
取3.14,求休闲广场的绿化率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点p第2019次碰到矩形的边时点P的坐标为( )
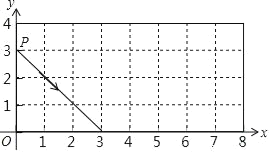
A. ( 1,4 )B. ( 5,0 )C. ( 8,3 )D. ( 6,4 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A是![]() 轴正半轴上一个定点,点P是函数
轴正半轴上一个定点,点P是函数![]() (
(![]() >0)上一个动点,PB⊥
>0)上一个动点,PB⊥![]() 轴于点B,连结PA,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
轴于点B,连结PA,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
A. 逐渐增大 B. 先增后减 C. 逐渐减小 D. 先减后增
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=150°,∠AOB=90°,OC平分∠MOB.
(1)如图1,若OA与OM重合时,求∠BON的度数;
(2)如图2,若∠AOC=35°,求∠BON的度数;
(3)当∠AOB绕点O逆时针旋转到如图3的位置,探究∠AOC与∠BON的数量关系,并说明理由.
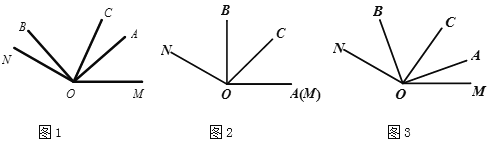
查看答案和解析>>
科目:初中数学 来源: 题型:
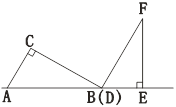
【题目】两个三角板ABC,DEF按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点、线都在同一平面内),其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=4 cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为![]() (cm),两个三角板重叠部分的面积为
(cm),两个三角板重叠部分的面积为![]() (cm2).
(cm2).
(1)当点C落在边EF上时,![]() =________cm;
=________cm;
(2)求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N,直接写出在三角板平移过程中,点M与点N之间距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蔬菜公司采购了若干吨的某种蔬菜,计划加工之后销售,若单独进行粗加工,需要20天才能完成;若单独进行精加工,需要30天才能完成,已知每天单独粗加工比单独精加工多生产10吨.
(1)求公司采购了多少吨这种蔬菜?
(2)据统计,这种蔬菜经粗加工销售,每吨利润2000元;经精加工后销售,每吨利润涨至2500元.受季节条件限制,公司必须在24天内全部加工完毕,由于两种加工方式不能同时进行,公司为尽可能多获利,安排将部分蔬菜进行精加工后,其余蔬菜进行粗加工,并恰好24天完成,加工的这批蔬菜若全部售出,求公司共获得多少元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
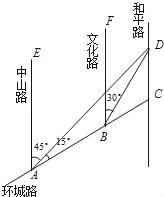
【题目】如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式![]() .
.
解∵![]() ,∴
,∴![]() 可化为
可化为![]() .
.
由有理数的乘法法则:两数相乘,同号得正,得:①![]() ②
②![]()
解不等式组①,得![]() ,解不等式组②,得
,解不等式组②,得![]()
∴![]() 的解集为
的解集为![]() 或
或![]() .
.
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)一元二次不等式![]() 的解集为____________;
的解集为____________;
(2)试解一元二次不等式![]() ;
;
(3)试解不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com