
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y=kx��ͼ���뷴��������y=![]() ��m��0����ͼ���ڵ�һ�����ڵ�C����ABC�DZ߳�Ϊ3�ĵȱ������Σ���AB����x����������ϣ�cos��COA=
��m��0����ͼ���ڵ�һ�����ڵ�C����ABC�DZ߳�Ϊ3�ĵȱ������Σ���AB����x����������ϣ�cos��COA=![]() ��
��
��1����k��m��ֵ��
��2����P������OC�ϣ���OP=5![]() ������Q�ӵ�P�����������ʵ���·���˶����߶�AB�д����ϵĵ�M�������ش�ֱ��y��ķ����˶���y���ϵĵ�N����������ʵ���·���˶�����A��ֹͣ������Q���˶�·�����ʱ����N�����꼰��Q�˶������·�̣�
������Q�ӵ�P�����������ʵ���·���˶����߶�AB�д����ϵĵ�M�������ش�ֱ��y��ķ����˶���y���ϵĵ�N����������ʵ���·���˶�����A��ֹͣ������Q���˶�·�����ʱ����N�����꼰��Q�˶������·�̣�
��3������ABC�Ƶ�A������ת������ת�����У���BC����ֱ��������OC�ཻ�ڵ�R����x�������ύ�ڵ�T������ORTΪ����������ʱ����OT�ij���

���𰸡���1��k=![]() ��m=
��m=![]() ��2��
��2��![]() +
+![]() ����3��OT�ij�Ϊ3+
����3��OT�ij�Ϊ3+![]()
![]() ��
��![]() ��3+
��3+![]() ��6��3��
��6��3��![]()
![]() +
+![]() ��
��
��������
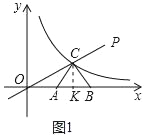
��1����cos��COA=![]() ���ɵ���AOC=30���������C���꼴�ɽ�����⣮
���ɵ���AOC=30���������C���꼴�ɽ�����⣮
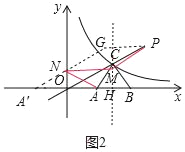
��2����ͼ2�У���CH��AB��H����PG��CH��ʹ��PG=OH������A����y��ĶԳƵ�A��������A��G��y����N����NM��y�ᣬ��CH��M����ʱ��Q�˶���·��P��M��N��A��̣�
����취���ֱ��A��G�Ľ���ʽ���ɽ�����⣮
��3���������������ۣ�����ͼ3�У���OR=OTʱ����AG��BC��G����AG=![]() ������ATG�Ŵ���ͼ4�У���AG��ȡһ��M��ʹ��AM=MT�������AT���ɣ�����ͼ5�У���RO=RTʱ����BG��AT��G������ͼ6�У���TO=TRʱ���ֱ���⼴�ɣ�
������ATG�Ŵ���ͼ4�У���AG��ȡһ��M��ʹ��AM=MT�������AT���ɣ�����ͼ5�У���RO=RTʱ����BG��AT��G������ͼ6�У���TO=TRʱ���ֱ���⼴�ɣ�
�⣺��1����ͼ1�У���CK��AB��K��
��cos��COA=![]() ��
��
���AOC=30�㣬
�ߡ�ABC�ǵȱ������Σ��߳�Ϊ3��
��AB=BC=AC=3����CAB=��CBA=��ACB=60�㣬
���BCO=90�㣬
��OB=2BC=6��OC=![]() ��
��
��CK=![]() OC=
OC=![]() ��OK=
��OK=![]() CK=
CK=![]() ��
��
���C���꣨![]() ��
��![]() �����ֱ��������������y=kx��ͼ���뷴��������y=
�����ֱ��������������y=kx��ͼ���뷴��������y=![]() ��
��
�ɵ�k=![]() ��m=
��m=![]() ��
��
��2����ͼ2�У���CH��AB��H����PG��CH��ʹ��PG=OH������A����y��ĶԳƵ�A��������A��G��y����N����NM��y�ᣬ��CH��M����ʱ��Q�˶���·��P��M��N��A��̣����ɣ�PM+MN+NA=PG+NG+A��N��=PG+A��G����PG=MN=�ų���A��G���߶Σ�����֮���߶���̣���PM+MN+NA��̣�
��OP=![]() �����P���꣨
�����P���꣨![]() ��
��![]() ����
����
��AH=![]() ��
��
��PG=MN=OH=![]() ��
��
��G��3��![]() ������A�䣨��3��0����
������A�䣨��3��0����
��ֱ��A��G�Ľ���ʽΪy=kx+b������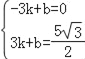 ��
��
���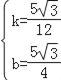 ��
��
��ֱ��A��N�Ľ���ʽΪy=![]() x+
x+![]() ��
��
���N���꣨0��![]() ����
����
��A��G=![]() =
=![]() ��
��
���Q�˶������·��=A��G+PG=![]() +
+![]() ��
��
��3������ͼ3�У���OR=OTʱ����AG��BC��G����AG=![]() ������ATG�Ŵ���ͼ4�У���AG��ȡһ��M��ʹ��AM=MT����
������ATG�Ŵ���ͼ4�У���AG��ȡһ��M��ʹ��AM=MT����
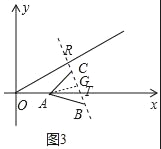
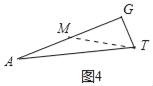
�ߡ�ATG=75�㣬��TAG=15�㣬
���A=��MTA=15�㣬
���TMG=30������GT=a����MT=AM=2a��MG=![]() a��
a��
��2a+![]() a=
a=![]() ��
��
��a=3![]() ��
��![]() ��
��
��AT=![]() =
=![]() =
=![]()
![]() ��
��![]()
![]() ��
��
��OT=3+![]()
![]() ��
��![]()
![]() ��
��
����ͼ5�У���RO=RTʱ����BG��AT��G��
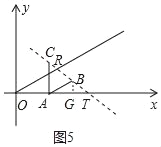
��RO=RT��
���ROT=��RTO=30�㣬
�ߡ�ABC=60��=��BAT+��BTA��
���BAT=��BTA=30�㣬
��BA=BT=3��AG=GT=ABcos30��=![]() ��
��
��AT=![]() ��OT=3+
��OT=3+![]() ��
��
����ͼ6�У���TO=TRʱ��
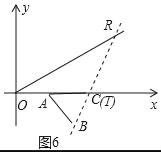
��TO=TR��
���TOR=��TRO=30�㣬
���OTR=120�㣬��ATR=60�㣬
��T��C�غϣ�
��OT=OA+AC=6��
����ͼ7�У��ɢڿ�֪����OR=OTʱ��OT=OA��AT=3��![]()
![]() +
+![]()
![]() ��
��
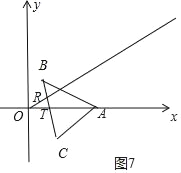
��������������ORTΪ����������ʱ��OT�ij�Ϊ3+![]()
![]() ��
��![]()
![]() ��3+
��3+![]() ��6��3��
��6��3��![]()
![]() +
+![]()
![]() ��
��


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ijУ���꼶(3)���һ��ѧϰС����в���Сɽ�߶ȵ�ʵ���������ͬѧ��ɽ��A�㴦���ɽ����һ��D������Ϊ30���������AD�ij���Ϊ180�ף���һ����ͬѧ��ɽ��B�㴦���ɽ��A��ĸ���Ϊ45����ɽ��D��ĸ���Ϊ60��������������Ǽ����Сɽ�ĸ߶�BC��(������̺ͽ������ȡ����ֵ)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���쳵������ͬʱ�Ӽس������Ը��Ե��ٶ��������ҵ���ʻ���쳵�����ҵغ�ͣ����45���ӣ�������ԭ·����һ�ٶ����ٷ��أ�ֱ����������������֪�������ٶ�Ϊ60ǧ��/ʱ������֮��ľ���y��ǧ�ף��������ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ����쳵���ҵط���ʱ���ٶ�Ϊ__________ǧ��/ʱ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ�����12�Ų�����һ�����ӣ�������12�ѣ����ִӼס������̳��˽ͬһ�ͺŵIJ������۶�Ϊÿ��200Ԫ�����α��۶�Ϊÿ��50Ԫ�����̳��涨��ÿ����һ�Ų�������һ�Ѳ��Σ����̳��涨�����в��������ξ������۵İ��������ۣ���ô��ʲô����µ����̳�������Żݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
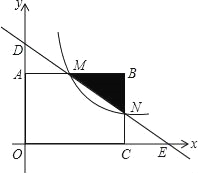
����Ŀ����ͼ����ֱ������ϵ�У�����OABC�Ķ���O������ԭ���غϣ�����A��C�ֱ����������ϣ�����B������Ϊ��4��2��������D��0��3����E��6��0����ֱ�߷ֱ���AB��BC���ڵ�M��N��
��1����ֱ��DE�Ľ���ʽ�͵�M�����ꣻ
��2��������������y=![]() ��x��0����ͼ����M���ڸ÷�����������ͼ�����Ƿ����һ��P��ʹ��PMN�����������OMN�������һ�룬�����ڣ����P�����꣬�������ڣ���˵�����ɣ�
��x��0����ͼ����M���ڸ÷�����������ͼ�����Ƿ����һ��P��ʹ��PMN�����������OMN�������һ�룬�����ڣ����P�����꣬�������ڣ���˵�����ɣ�
��3��������������y=![]() ��x��0����ͼ������MNB�й����㣬��ֱ��д��m��ȡֵ��Χ��
��x��0����ͼ������MNB�й����㣬��ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
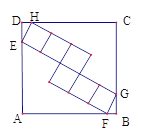
����Ŀ����ͼ��������ABCD�У��ڲ���6��ȫ�ȵ������Σ�С�����εĶ���E��F��G��H�ֱ��ڱ�AD��AB��BC��CD�ϣ���tan��DEH=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��˫����y����![]() �ڵڶ�����֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ����������ABC���ҡ�ACB��120������C�ڵ�һ���ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����y��
�ڵڶ�����֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ����������ABC���ҡ�ACB��120������C�ڵ�һ���ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����y��![]() ���˶�����k��ֵΪ_____��
���˶�����k��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
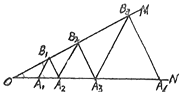
����Ŀ����ͼ����֪��![]() ����
����![]() ��
��![]() ��
��![]() ��������
��������![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ��������
��������![]() �ϣ�
�ϣ�![]() ��
��![]() ��
��![]() ����Ϊ�ȱ������Σ���
����Ϊ�ȱ������Σ���![]() ����
����![]() �ı߳�Ϊ�� ��
�ı߳�Ϊ�� ��
A.6B.12C.32D.64
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB�ǡ�O��ֱ������CD��AB�ཻ����BAC��40�㣮
��1����ͼ1����DΪ��AB���е㣬���ABC�͡�ABD�Ķ�����
��2����ͼ2������D����O�����ߣ���AB���ӳ��߽��ڵ�P����DP��AC�����OCD�Ķ�����
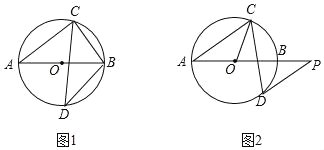
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com