Question

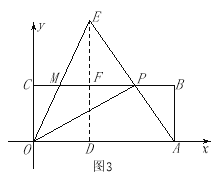
【题目】如图，在直角坐标系中，矩形的顶点、分别在轴和轴正半轴上，点的坐标是，点是边上一动点（不与点、点重合），连结、，过点作射线交的延长线于点，交边于点，且，令，.

（1）当为何值时，？

（2）求与的函数关系式，并写出的取值范围；

（3）在点的运动过程中，是否存在，使的面积与的面积之和等于的面积.若存在，请求的值；若不存在，请说明理由.

Answer 1

【答案】（1）当时，；（2）（）；（3）存在，.

【解析】

试题分析：（1）由题意可知，当OP⊥AP时，∽，∴，即，于是解得x值；（2）根据已知条件利用两角对应相等两个三角形相似，证明三角形OCM和三角形PCO相似,得出对应边成比例即可得出结论；（3）假设存在x符合题意. 过作于点，交于点，由与面积之和等于的面积，∴.然后求出ED，EF的长，再根据三角形相似：∽，求出MP的长，进而由上题的关系式求出符合条件的x.

试题解析：（1）证明三角形OPC和三角形PAB相似是解决问题的关键，由题意知，，BC∥OA,∵，∴.∴.∴∽,∴，即，解得（不合题意,舍去）. ∴当时，；(2)由题意可知，∥，∴.∵（已知），∴. ∵，∴∽，∴对应边成比例：，即. ∴，因为点是边上一动点（不与点、点重合），且满足∽，所以的取值范围是.（3）假设存在符合题意. 如图所示，过作于点，交于点， 则.∵与面积之和等于的面积，∴. ∴. ∵∥，∴∽. ∴. 即，解得. 因为由（2）得，所以. 解得（不合题意舍去）. ∴在点的运动过程中存在x,，使与面积之和等于的面积，此时.