
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】冬至过后,昼夜温差逐渐加大,山城的市民们已然感受到了深冬的寒意.在还未普遍使用地暖供暖设备的山城,小型电取暖器仍然深受市民的青睐.某格力专卖店销售壁挂式电暖器和卤素/石英式取暖器(俗称 “小太阳”),其中壁挂式电暖器的售价是“小太阳”售价的5倍还多100元,2016年12月份壁挂式电暖器和“小太阳”共销售500台,壁挂式电暖器与“小太阳”销量之比是4∶1,销售总收入为58.6万元.
(1)分别求出每台壁挂式电暖器和“小太阳”的售价;
(2)随着“元旦、春节”双节的来临和气温的回升,销售进入淡季,2017年1月份,壁挂式电暖器的售价比2016年12月下调了4m﹪,根据经验销售量将比2016年12月下滑6m﹪,而“小太阳”的销售量和售价都维持不变,预计销售总收入将下降到16.04万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2(a≠0)与直线y=2x-3交于点A(1,b),求:
(1)a和b的值;
(2)求抛物线y=ax2的顶点和对称轴;
(3)x取何值时,二次函数y=ax2中的y随x的增大而增大;
查看答案和解析>>
科目:初中数学 来源: 题型:
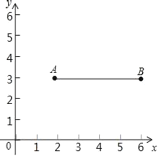
【题目】在平面直角坐标系中,已知点A(2,3),B(6,3),连接AB,如果点P在直线y=x﹣1上,且点P到直线AB的距离小于1,那么称点P是线段AB的“临近点”,则下列点为AB的“临近点”的是( )
A.(![]() ,
,![]() )B.(3,3)C.(6,5)D.(1,0)
)B.(3,3)C.(6,5)D.(1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳阳王家河流域综合治理工程已正式启动,其中某项工程,若由甲、乙两建筑队合做,6个月可以完成,若由甲、乙两队独做,甲队比乙队少用5个月的时间完成.
(1)甲、乙两队单独完成这项工程各需几个月的时间?
(2)已知甲队每月施工费用为15万元,比乙队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲队做a个月,乙队做b个月(a、b均为整数)分工合作的方式施工,问有哪几种施工方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象经过(0,3),(4,3).
(1)求b、c的值.
(2)开口方向 ,对称轴为 ,顶点坐标为 .
(3)该函数的图象怎样由y=x2的图象平移得到.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com